В этом разделе приведено несколько примеров определения большого О для операторов повторения, последовательности и выбора.

Пример 1

Учитывайте временную сложность следующего цикла:

for (int i = 1; i к = к 5;
}

Это постоянное время c для выполнения

k = k 5;

Поскольку цикл выполняется n раз, временная сложность цикла равна

T(n) = (константа c)*n = O(n).

Теоретический анализ предсказывает производительность алгоритма. Чтобы увидеть, как работает этот алгоритм, мы запустим код в программе ниже, чтобы получить время выполнения для n = 1000000, 10000000, 100000000 и 100000000.

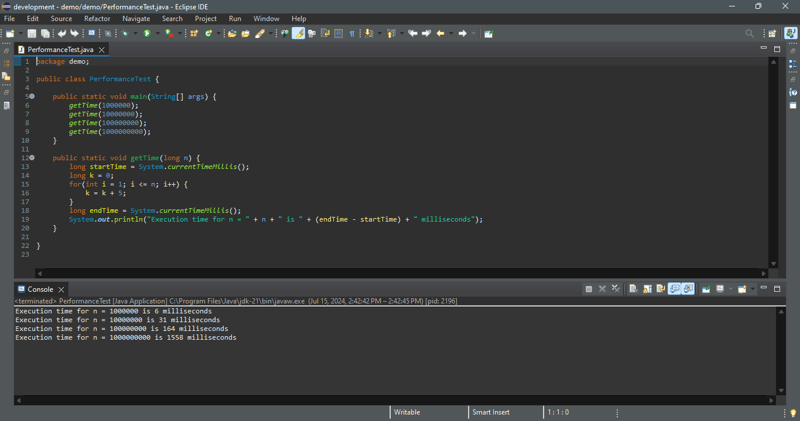
Наш анализ предсказывает линейную временную сложность для этого цикла. Как показано в примере выходных данных, когда размер входных данных увеличивается в 10 раз, время выполнения увеличивается примерно в 10 раз. Исполнение подтверждает предсказание.

Пример 2

Какова временная сложность следующего цикла?

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Это постоянное время c для выполнения

k = k i j;

Внешний цикл выполняется n раз. Для каждой итерации внешнего цикла внутренний цикл выполняется n раз. Таким образом, временная сложность цикла равна

T(n) = (константа c)*n*n = O(n^2)

Алгоритм с временной сложностью O(n^2) называется квадратичным алгоритмом и демонстрирует квадратичную скорость роста. Квадратичный алгоритм быстро растет по мере увеличения размера задачи. Если вы удвоите размер входных данных, время работы алгоритма увеличится в четыре раза. Алгоритмы с вложенным циклом часто являются квадратичными.

Пример 3

Рассмотрим следующий цикл:

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Внешний цикл выполняется n раз. Для i = 1, 2, c внутренний цикл выполняется один раз, два раза и n раз. Таким образом, временная сложность цикла равна

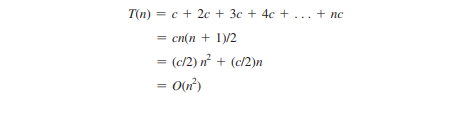
Пример 4

Рассмотрим следующий цикл:

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Внутренний цикл выполняется 20 раз, а внешний цикл n раз. Следовательно, временная сложность цикла равна

T(n) = 20*c*n = O(n)

Пример 5

Рассмотрим следующие последовательности:

for (int j = 1; j к = к 4;
}

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

Первый цикл выполняется 10 раз, а второй 20 * n раз. Таким образом, временная сложность цикла равна

T(n) = 10*c 20*c*n = O(n)

Пример 6

Рассмотрим следующий оператор выбора:

if (list.contains(e)) {
System.out.println(e);
}
еще
for (Объект t: список) {
System.out.println(t);
}

Предположим, список содержит n элементов. Время выполнения для list.contains(e) равно O(n). Цикл в предложении else занимает время O(n). Следовательно, временная сложность всего оператора равна

Пример 7

Рассмотрим вычисление a^n для целого числа n. Простой алгоритм умножит n раз следующим образом:

результат = 1;
for (int i = 1; i результат *= а;

Алгоритм занимает время O(n). Без ограничения общности предположим, что n = 2^k. Улучшить алгоритм можно по следующей схеме:

результат = a;
for (int i = 1; i результат = результат * результат;

Алгоритм занимает время O(logn). Для произвольного n вы можете пересмотреть алгоритм и доказать, что сложность по-прежнему равна O(logn).

Для простоты, поскольку 0(logn) = 0(log2n) = 0(logan), постоянная база опущена.