Разработка алгоритма заключается в разработке математического процесса решения проблемы. Анализ алгоритма предназначен для прогнозирования производительности алгоритма. В предыдущих двух главах были представлены классические структуры данных (списки, стеки, очереди, очереди с приоритетами, наборы и карты) и применены их для решения проблем. В этой главе на различных примерах будут представлены общие алгоритмические методы (динамическое программирование, принцип «разделяй и властвуй» и возврат с возвратом) для разработки эффективных алгоритмов.

Обозначение Big O позволяет получить функцию для измерения временной сложности алгоритма на основе размера входных данных. Вы можете игнорировать мультипликативные константы и недоминирующие члены в функции. Предположим, что два алгоритма выполняют одну и ту же задачу, например поиск (линейный поиск или бинарный поиск). Какая из них лучше? Чтобы ответить на этот вопрос, вы можете реализовать эти алгоритмы и запустить программы, чтобы получить время выполнения. Но с этим подходом есть две проблемы:

• Во-первых, на компьютере одновременно выполняется множество задач. Время выполнения конкретной программы зависит от загрузки системы.
• Во-вторых, время выполнения зависит от конкретного ввода. Рассмотрим, например, линейный поиск и бинарный поиск. Если элемент, который нужно найти, оказывается первым в списке, линейный поиск найдет элемент быстрее, чем двоичный поиск.

Очень сложно сравнивать алгоритмы, измеряя время их выполнения. Чтобы преодолеть эти проблемы, был разработан теоретический подход для анализа алгоритмов, независимых от компьютеров и конкретных входных данных. Этот подход аппроксимирует влияние изменения на размер входных данных. Таким образом, вы можете увидеть, насколько быстро увеличивается время выполнения алгоритма с увеличением размера входных данных, поэтому вы можете сравнить два алгоритма, исследуя их скорости роста.

Рассмотрим линейный поиск. Алгоритм линейного поиска последовательно сравнивает ключ с элементами массива, пока ключ не будет найден или массив не будет исчерпан. Если ключа нет в массиве, требуется сравнение n для массива размером n. Если ключ находится в массиве, в среднем требуется n/2 сравнений. Время выполнения алгоритма пропорционально размеру массива. Если вы удвоите размер массива, вы ожидаете, что количество сравнений удвоится. Алгоритм растет с линейной скоростью. Темп роста имеет порядок n. Ученые-компьютерщики используют обозначение Big O для обозначения «порядка величины». Используя эти обозначения, сложность алгоритма линейного поиска равна O(n), что произносится как «порядка n». Мы называем алгоритм с временной сложностью O(n) линейным алгоритмом, и он демонстрирует линейную скорость роста.

Для одного и того же размера входных данных время выполнения алгоритма может различаться в зависимости от входных данных. Входные данные, которые приводят к наименьшему времени выполнения, называются входными данными для наилучшего случая, а входные данные, которые приводят к наибольшему времени выполнения, называются входными данными для входными данными для наихудшего случая. Анализ наилучшего случая и
Анализ наихудшего случая заключается в анализе алгоритмов на предмет их входных данных в лучшем и худшем случае. Анализ наилучшего и наихудшего случая не является репрезентативным, но анализ наихудшего случая очень полезен. Вы можете быть уверены, что алгоритм никогда не будет медленнее, чем в худшем случае.
Анализ среднего случая пытается определить среднее количество времени среди всех возможных входных данных одинакового размера. Анализ среднего случая идеален, но его сложно выполнить, поскольку для многих задач трудно определить относительные вероятности и распределения различных входных данных. Анализ наихудшего случая выполнить легче, поэтому анализ обычно проводится для наихудшего случая.

Алгоритм линейного поиска требует сравнений n в худшем случае и сравнений n/2 в среднем случае, если вы почти всегда ищете что-то, что известно о наличии в списке. Используя обозначение Big O, в обоих случаях требуется время O(n). Мультипликативную константу (1/2) можно опустить. Анализ алгоритма ориентирован на скорость роста. Мультипликативные константы не влияют на темпы роста. Темп роста для n/2 или 100_n_ такой же, как и для n, как показано в таблице ниже, Темпы роста. Следовательно, O(n) = O(n/2) = O(100n).

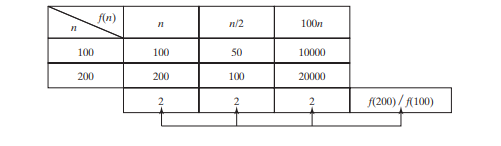
Рассмотрим алгоритм поиска максимального числа в массиве из n элементов. Чтобы найти максимальное число, если n равно 2, требуется одно сравнение; если n равно 3, два сравнения. В общем случае требуется n–1 сравнений, чтобы найти максимальное число в списке из n элементов. Анализ алгоритма предназначен для большого размера входных данных. Если размер входных данных невелик, оценка эффективности алгоритма не имеет значения. По мере увеличения n часть n в выражении n - 1 доминирует над сложностью. Обозначение Big O позволяет игнорировать недоминирующую часть (например, -1 в
выражение n - 1) и выделите важную часть (например, n в выражении n - 1). Следовательно, сложность этого алгоритма равна O(n).

Обозначение Big O оценивает время выполнения алгоритма в зависимости от размера входных данных. Если время не связано с размером входных данных, говорят, что алгоритм использует постоянное время с обозначением O(1). Например, метод, который извлекает элемент по заданному индексу в массиве
занимает постоянное время, поскольку время не увеличивается с увеличением размера массива.

Следующие математические суммирования часто полезны при анализе алгоритмов:

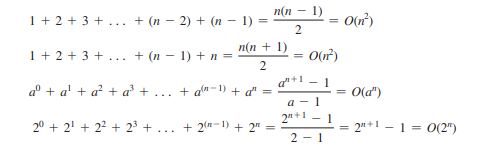
Временная сложность — это мера времени выполнения с использованием нотации Big-O. Аналогичным образом вы также можете измерить пространственную сложность, используя нотацию Big-O. Пространственная сложность измеряет объем памяти, используемый алгоритмом. Пространственная сложность большинства алгоритмов, представленных в книге, равна O(n). т. е. они демонстрируют линейную скорость роста входного размера. Например, пространственная сложность линейного поиска равна O(n).