Поиск в глубину графа начинается с вершины графа и посещает все вершины графа, насколько это возможно, перед возвратом.
Поиск в глубину графа аналогичен поиску в глубину дерева, обсуждаемому в разделе «Обход дерева», «Обход дерева». В случае дерева поиск начинается с корня. В графе поиск может начинаться с любой вершины.

Поиск в глубину дерева сначала посещает корень, затем рекурсивно посещает поддеревья корня. Аналогично, поиск в глубину графа сначала посещает вершину, а затем рекурсивно посещает все вершины, смежные с этой вершиной. Разница в том, что граф может содержать циклы, что может привести к бесконечной рекурсии. Чтобы избежать этой проблемы, вам необходимо отслеживать уже посещенные вершины.

Поиск называется сначала в глубину, потому что он ищет «глубже» в графе как можно глубже. Поиск начинается с некоторой вершины v. После посещения v он посещает непосещенного соседа v. Если у v нет непосещенного соседа, поиск возвращается к вершине, из которой он достиг v. Мы предполагаем, что граф связен и начинается поиск. из любой вершины можно достичь всех вершин.

Алгоритм поиска в глубину

Алгоритм поиска в глубину описан в коде ниже.

Ввод: G = (V, E) и начальная вершина v
Выход: дерево DFS с корнем в v
1 Дерево dfs(вершина v) {
2 визита v;
3 для каждого соседа w ​​из v
4 if (w не был посещен) {
5 установить v в качестве родителя для w в дереве;
6 дфс(ж);
7 }
8 }

Вы можете использовать массив с именем isVisited для обозначения того, была ли посещена вершина. Первоначально isVisited[i] имеет значение false для каждой вершины i. После посещения вершины, скажем, v, параметру isVisited[v] присваивается значение true.

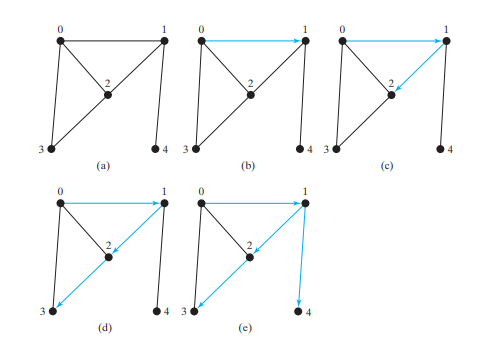
Рассмотрим график на рисунке ниже (a). Предположим, мы начинаем поиск в глубину с вершины 0. Сначала посещаем вершину 0, затем любого из ее соседей, скажем, 1. Теперь посещаем вершину 1, как показано на рисунке ниже (b). У вершины 1 три соседа — 0, 2 и 4. Поскольку вершина 0 уже была посещена, вы посетите либо 2, либо 4. Давайте выберем 2. Теперь вершина 2 посещена, как показано на рисунке ниже (c). У вершины 2 есть три соседа: 0, 1 и 3. Поскольку вершины 0 и 1 уже были посещены, выберите вершину 3. Теперь вершина 3 посещена, как показано на рисунке ниже (d). На данный момент вершины посещены в следующем порядке:

0, 1, 2, 3

Поскольку все соседи вершины 3 были посещены, вернитесь к вершине 2. Поскольку все вершины вершины 2 были посещены, вернитесь к вершине 1. 4 смежна с 1, но вершина 4 не была посещена. Поэтому посетите пункт 4, как показано на рисунке ниже (e). Поскольку все соседи числа 4 посещены, вернитесь к 1.
Поскольку все соседи 1 были посещены, вернитесь к 0. Поскольку все соседи 0 были посещены, поиск заканчивается.

Поскольку каждое ребро и каждая вершина посещаются только один раз, временная сложность метода dfs равна O(|E| |V|), где |E | обозначает количество ребер, а |V| количество вершин.

Реализация поиска в глубину

Алгоритм DFS в приведенном выше коде использует рекурсию. Для его реализации естественно использовать рекурсию. Альтернативно вы можете использовать стек.

Метод dfs(int v) реализован в строках 164–193 в AbstractGraph.java. Он возвращает экземпляр класса Tree с вершиной v в качестве корня. Метод сохраняет искомые вершины в списке searchOrder (строка 165), родительском элементе каждой вершины в массиве parent (строка 166) и использует isVisited массив, указывающий, была ли посещена вершина (строка 171). Он вызывает вспомогательный метод dfs(v, родитель, searchOrder, isVisited) для выполнения поиска в глубину (строка 174).

В рекурсивном вспомогательном методе поиск начинается с вершины u. u добавляется в searchOrder в строке 184 и помечается как посещенный (строка 185). Для каждого непосещенного соседа u метод рекурсивно вызывается для выполнения поиска в глубину. При посещении вершины e.v родительский элемент e.v сохраняется в parent[e.v] (строка 189). Метод возвращается, когда посещены все вершины связного графа или связного компонента.

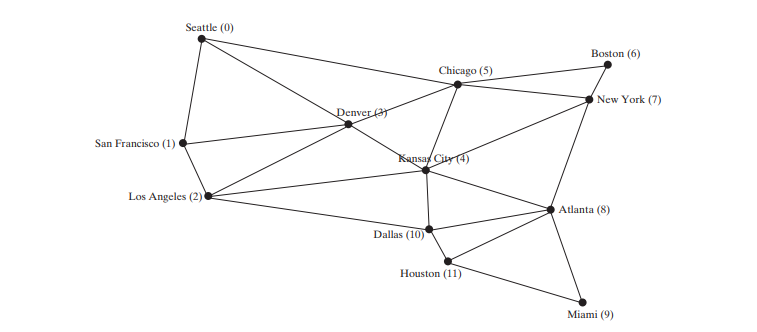
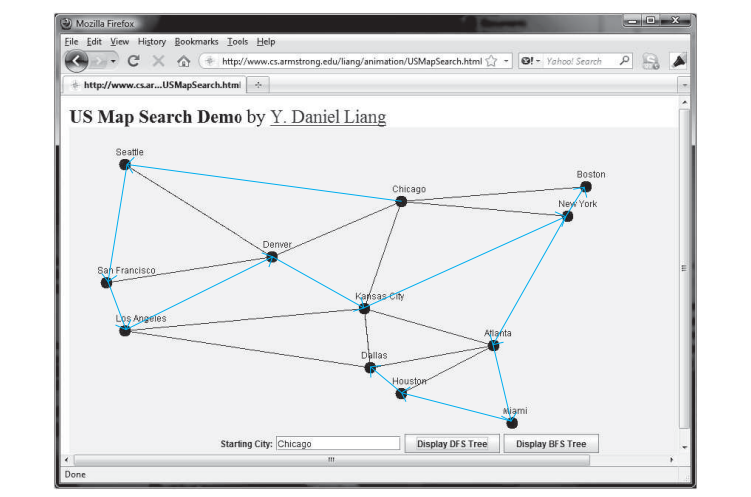
Приведенный ниже код представляет собой тестовую программу, которая отображает DFS для графа на рисунке выше, начиная с Чикаго. Графическая иллюстрация DFS, начиная с Чикаго, показана на рисунке ниже.

public class TestDFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph graph = new UnweightedGraph(vertices, edges);
        AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago"));

        java.util.List searchOrders = dfs.getSearchOrder();
        System.out.println(dfs.getNumberOfVerticesFound()   " vertices are searched in this DFS order:");
        for(int i = 0; i 



В этом порядке DFS ищется 12 вершин:

 Чикаго Сиэтл Сан-Франциско Лос-Анджелес Денвер

 Канзас-Сити Нью-Йорк Бостон Атланта Майами Хьюстон Даллас

родитель Сиэтла - Чикаго

родитель Сан-Франциско — Сиэтл

родитель Лос-Анджелеса — Сан-Франциско

родитель Денвера — Лос-Анджелес

родитель Канзас-Сити - Денвер

родитель Бостона — Нью-Йорк

Родитель Нью-Йорка — Канзас-Сити

Родитель Атланты - Нью-Йорк

родитель Майами — Атланта

родитель Далласа - Хьюстон

родитель Хьюстона — Майами




  
  
  Приложения ДФС


Поиск в глубину можно использовать для решения многих проблем, например следующих:

Определение связности графа. Найдите граф, начиная с любой вершины. Если количество искомых вершин совпадает с количеством вершин в графе, граф связен. В противном случае граф не связен.
Определение наличия пути между двумя вершинами.
Нахождение пути между двумя вершинами.
Нахождение всех подключенных компонентов. Компонент связности — это максимальный связный подграф, в котором каждая пара вершин соединена путем.
Определение наличия цикла в графике.
Нахождение цикла на графике.
Нахождение гамильтонова пути/цикла. Гамильтонов путь в графе — это путь, который посещает каждую вершину графа ровно один раз. Гамильтонов цикл посещает каждую вершину графа ровно один раз и возвращается в начальную вершину.
Первые шесть проблем можно легко решить с помощью метода dfs в AbstractGraph.java. Чтобы найти гамильтонов путь/цикл, вам необходимо изучить все возможные DFS, чтобы найти тот, который ведет к самому длинному пути. Гамильтонов путь/цикл имеет множество приложений, в том числе для решения известной проблемы «Рыцарского тура».