Вы когда-нибудь задумывались, почему казино всегда выигрывают? В статье «Преодоление шансов: математика, лежащая в основе прибыли казино» мы рассмотрим простую математику и умные стратегии, которые позволяют казино зарабатывать деньги в долгосрочной перспективе. С помощью простых для понимания примеров и моделирования Монте-Карло мы раскроем секреты края дома. Приготовьтесь узнать, как казино меняют шансы в свою пользу!

Понимание преимущества казино

Преимущество казино — фундаментальная концепция в мире казино. Он представляет собой среднюю прибыль, которую казино ожидает получить от каждой ставки, сделанной игроками. По сути, это процент от каждой ставки, который казино сохранит в долгосрочной перспективе.

Преимущество казино существует потому, что казино не выплачивают выигрышные ставки в соответствии с «истинными шансами» игры. Истинные шансы представляют собой фактическую вероятность наступления события. Выплачивая выплаты по немного более низким коэффициентам, казино гарантируют, что со временем получат прибыль.

Преимущество казино (HE) определяется как прибыль казино, выраженная в процентах от первоначальной ставки игрока.

** Европейская рулетка ** имеет только один зеленый ноль, всего в ней 37 номеров. Если игрок ставит 1 доллар на красное, у него есть шанс 18/37 выиграть 1 доллар и шанс 19/37 проиграть 1 доллар. Ожидаемое значение:

Ожидаемая стоимость=( 1 × 18/37 ​) ( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≈ −2,7%

Следовательно, в европейской рулетке преимущество казино (HE) составляет около 2,7%.

Давайте создадим собственную игру, чтобы лучше понять ее: простую игру с бросками кубиков.

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll 

В этой игре:

• У игрока есть шанс проиграть 1/100, если выпало 100.

• Шанс игрока на проигрыш составляет 50/100, если результат броска находится в диапазоне от 1 до 50.

• Шанс игрока на победу составляет 49/100, если результат броска составляет от 51 до 99.

Ожидаемая стоимость =(1× 49/100​) ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100 ​ ≈ −2%

Следовательно, преимущество казино составляет 2%.

Понимание моделирования Монте-Карло

Моделирование Монте-Карло — это мощный инструмент, используемый для понимания и прогнозирования сложных систем путем проведения многочисленных симуляций процесса и наблюдения за результатами. В контексте казино моделирование Монте-Карло может моделировать различные сценарии ставок, чтобы показать, как преимущество казино обеспечивает долгосрочную прибыльность. Давайте рассмотрим, как работают симуляции Монте-Карло и как их можно применить к простой игре в казино.

Что такое моделирование Монте-Карло?

Моделирование Монте-Карло включает в себя генерацию случайных величин для многократного моделирования процесса и анализ результатов. Выполняя тысячи или даже миллионы итераций, мы можем получить распределение возможных результатов и получить представление о вероятности различных событий.

Применение моделирования Монте-Карло к игре в кости

Мы воспользуемся симуляцией Монте-Карло для моделирования игры с бросками костей, о которой мы говорили ранее. Это поможет нам понять, как преимущество казино влияет на прибыльность игры с течением времени.

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins  = 1
        else:
            losses  = 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

Интерпретация результатов

В этой симуляции мы запускаем игру с бросками костей 10 000 000 раз, чтобы наблюдать проценты выигрышей и проигрышей. Учитывая рассчитанное ранее преимущество казино (2%), мы ожидаем, что процент потерь будет немного выше, чем процент выигрышей.

После запуска моделирования вы можете увидеть такие результаты:

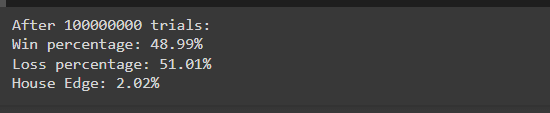
Эти результаты тесно согласуются с теоретическими вероятностями (49% выигрыша, 51% проигрыша), демонстрируя, как преимущество казино проявляется в большом количестве попыток. Небольшой дисбаланс обеспечивает прибыльность казино в долгосрочной перспективе.

Визуализация краткосрочных побед и долгосрочных потерь

Моделирование Монте-Карло является мощным средством моделирования и прогнозирования результатов посредством повторной случайной выборки. В контексте азартных игр мы можем использовать моделирование Монте-Карло, чтобы понять потенциальные результаты различных стратегий ставок.

Мы смоделируем одного игрока, который делает одну и ту же начальную ставку в каждом раунде, и посмотрим, как меняется стоимость его счета в течение определенного количества ставок.

Вот как мы можем смоделировать и визуализировать процесс ставок с помощью Matplotlib:

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager 



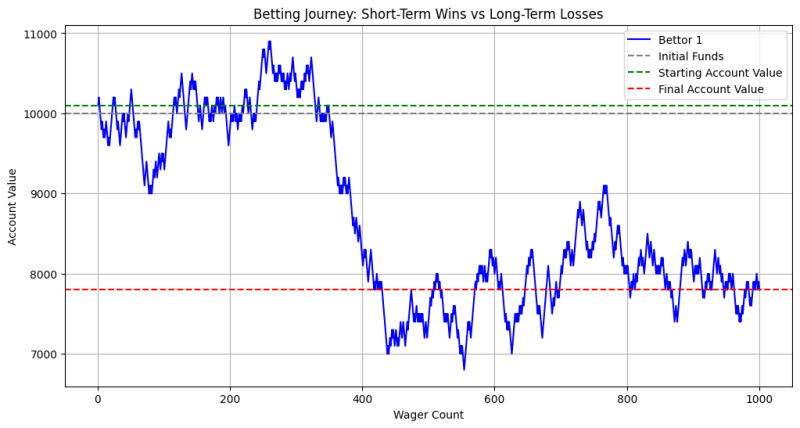
На этом графике показано, как стоимость счета игрока может меняться с течением времени в зависимости от выигрышей и поражений. Первоначально могут быть периоды выигрыша (зеленая линия над стартовым значением), но по мере увеличения количества ставок кумулятивный эффект преимущества казино становится очевидным. В конечном итоге стоимость счета игрока имеет тенденцию снижаться до или ниже начальных средств (серая линия), что указывает на долгосрочные потери.


  
  
  Заключение


Понимание математики, лежащей в основе прибыли казино, показывает явное преимущество казино в каждой игре благодаря концепции преимущества казино. Несмотря на случайные выигрыши, вероятность, заложенная в игры казино, гарантирует, что большинство игроков со временем потеряют деньги. Моделирование Монте-Карло ярко иллюстрирует эту динамику, показывая, как даже краткосрочные выигрыши могут маскировать долгосрочные потери из-за статистического преимущества казино. Такое понимание математической достоверности прибыльности казино подчеркивает важность принятия обоснованных решений и ответственной практики азартных игр.

Далее мы могли бы изучить дополнительные визуализации или варианты, такие как сравнение различных стратегий ставок или анализ влияния различных первоначальных ставок на результаты игрока.

Оставайся на связи:

• GitHub: ezhillragesh

• Твиттер: ezhillragesh

• Сайт: ragesh.me

Не стесняйтесь делиться своими мыслями, задавать вопросы и участвовать в обсуждении.

Удачного программирования!