Imagine se você pudesse usar apenas linhas retas, elipses e círculos, não seria difícil projetar um carro com linhas suaves e uma aparência complexa?

Em 1962, o engenheiro francês Pierre Bézier publicou a curva de Bézier, que foi inicialmente usada para o projeto da carroceria principal dos carros.

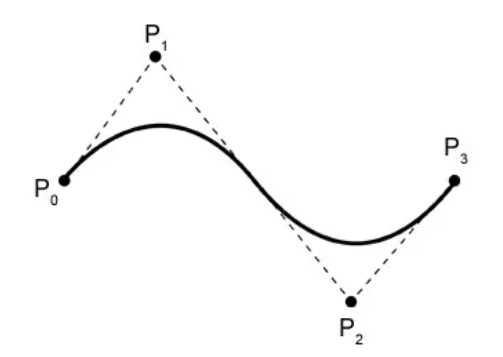
As curvas de Bézier podem definir uma curva suave através de uma série de pontos de controle. A curva sempre passa pelo primeiro e último pontos de controle e é influenciada pela forma dos pontos de controle intermediários. Além disso, as curvas de Bézier têm a propriedade de cascas convexas.

As curvas de Bézier são amplamente utilizadas em computação gráfica e modelagem de imagens, como em animação, design de fontes e design industrial.

Fórmula

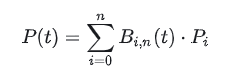
Vamos entender isso.

P(t) representa um ponto na curva em t (t é uma fração, com valor de 0 a 1). O que é um ponto na curva em t? Uma descrição comum da curva é: y = f(x), e por enquanto, vamos entender P(t) como f(x). A diferença é que P(t) é uma representação paramétrica (e o resultado do cálculo é um "vetor" como [x, y]), que será explicado em detalhes posteriormente.

Em seguida, Pi representa o i-ésimo ponto de controle (i começa em 0). Tomando como exemplo a figura acima, existem 4 pontos de controle, que são P0, P1, P2, P3. O n na fórmula é o último índice dos pontos de controle, ou seja, n = 3 (observe que não é o número de pontos de controle, mas sim a contagem menos 1).

Bi,n(t) é a função base de Bernstein, também conhecida como função base. Para cada (i, n) específico existe uma função base diferente correspondente a ele. Se você entender de uma perspectiva ponderada, poderá considerar a função de base como uma função de peso, indicando a "contribuição" do i-ésimo ponto de controle Pi para as coordenadas da curva na posição de t.

A fórmula para a função base é a seguinte:

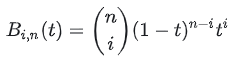
$\left(\genfrac{}{}{0px}{}{n}{i}\right)$( in​) É o número da combinação (quantas maneiras de escolher i entre n?). Quanto ao motivo da função base ter esta aparência, ela pode ser entendida em conexão com o algoritmo De Casteljau (veja mais adiante no texto)

De volta à fórmula P(t), ${\sum }_{i=0}^n$∑i=0n ​ é o símbolo de soma, indicando que a parte subsequente ( $B_{i,n}(t)\cdot P_i$Bi,n​(t )⋅Pi​ ) deve ser somado de i=0 a i=n.

Tomando a figura acima como exemplo, supondo que queremos calcular P(0,1), como fazer? É expandido da seguinte forma:

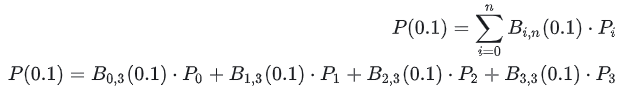
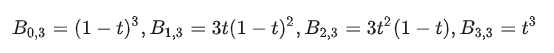
Substitua t=0,1 para obter:

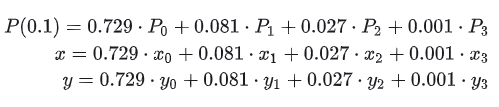
Representação paramétrica da curva

Aqui cita diretamente um artigo de um internauta (link)

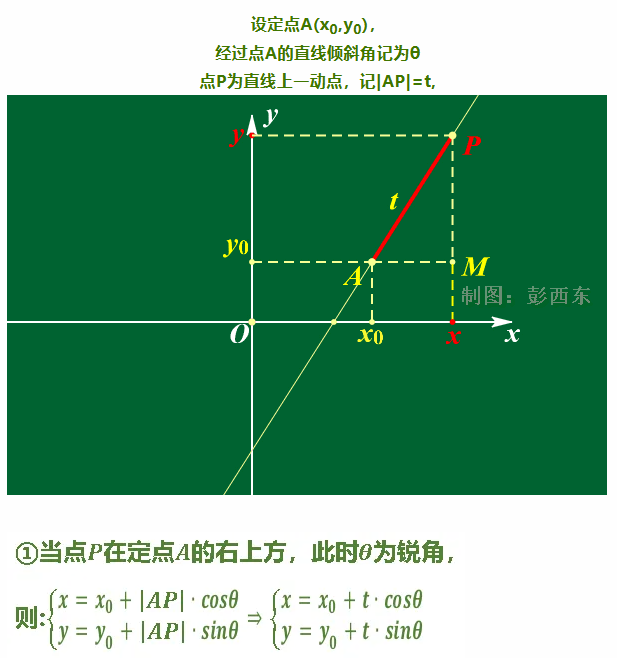
Vamos nos concentrar na fórmula acima.

Como mostrado na figura acima, a linha reta que conhecemos pode ser entendida de outra perspectiva: usando t (ou seja, o comprimento de |AP| do ponto P ao ponto conhecido (x0,y0)), então o ponto P pode ser determinado através das funções trigonométricas acima.

Mais geralmente, pode ser escrito como:

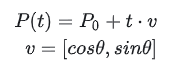
Aqui, P0 é o vetor [x0,y0]e v também é um vetor. Quando somados, P(t)é o vetor [x,y].

Olhando para o círculo novamente:

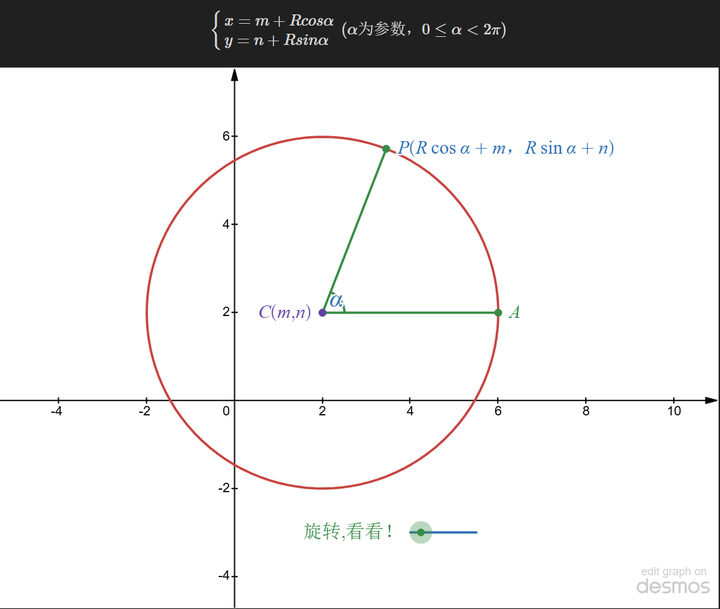
Conforme mostrado no diagrama, o círculo pode ser visto como tendo um centro conhecido, com qualquer ponto do círculo sendo determinado pelo ângulo de rotação e pelo raio. Também pode ser escrito como:

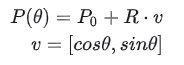
As equações paramétricas mantêm a invariância geométrica e podem representar formas como círculos (onde um x corresponde a vários valores de y).

De Casteljau

O algoritmo De Casteljau é um método usado em aplicações práticas para avaliar e aproximar curvas de Bézier para desenho e outras operações. Comparado ao método de avaliação anterior baseado em definição, é mais rápido e estável, e mais próximo das características das curvas de Bézier.

Aqui, nos referimos a dois artigos: link1 e link2

Em primeiro lugar, é definido o seguinte:

Veja o β acima. É um pouco confuso com os sobrescritos e subscritos; você pode usar a seguinte recursão triangular para compreensão:

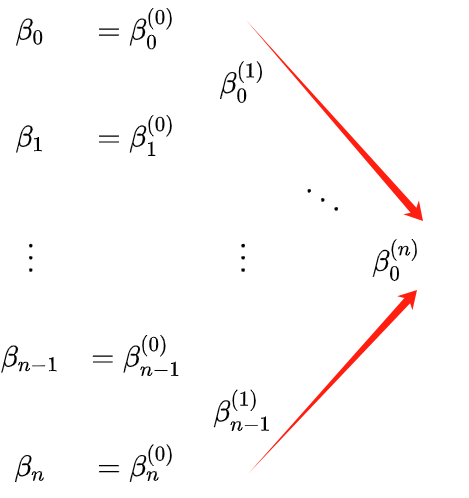
As bordas vermelhas do triângulo na figura acima são os pontos de controle dos dois segmentos divididos por t0. Para entender mais vividamente t0, P(t0) （ou seja, ${\beta }_0^{(n)}$β0(n)​ ）, os pontos de controle das duas curvas, você pode consultar a figura a seguir:

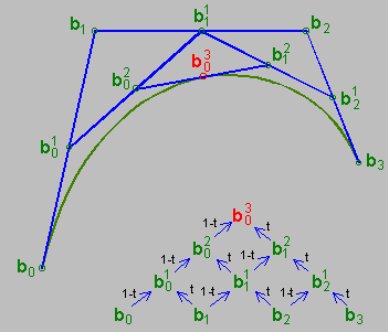
A figura acima demonstra as relações entre vários pontos quando t=0,5.

Na perspectiva da "interpolação", o processo de cálculo também pode ser entendido como:

1. Encontrar os pontos médios de cada par de pontos de controle adjacentes (porque t=0,5), ou seja, b01, b11, b21 (por favor, perdoe minha notação; escrever em LaTeX é muito problemático)
2. Encontre o ponto médio b02 em b01−b11 e encontre o ponto médio b12 em b11-b21
3. Encontre o ponto médio b03 em b02−b12 ​ Na verdade, a essência do algoritmo De Casteljau é interpolação e iteração.

Desenho de curva baseado em De Casteljau

Atualmente, dois métodos são observados.

Um método envolve percorrer t de 0 a 1 com pequenos incrementos de passo (ou seja, 0,01). Cada vez que P(t) é procurado, uma fórmula recursiva é usada para determinar ${\beta }_0^{(n)}$β0(n)​ .

O outro método envolve buscar P(t=0,5), e então para as duas curvas divididas, P(t=0,5) é buscado respectivamente... Esta subdivisão continua até que a curva seja aproximada.

Implementação

Sempre parece irreal apenas assistir sem praticar.

Então escrevi meu próprio código de implementação para desenho de curvas e o organizei em um kit de ferramentas: Compilelife's Toolkit

O código principal correspondente está aqui