Introdução 1

O processo no qual uma função chama a si mesma é chamado de recursão e o
a função correspondente é chamada de função recursiva.
Visto que a programação de computadores é uma aplicação fundamental da matemática, então vamos
primeiro tentemos entender o raciocínio matemático por trás da recursão.
Em geral, todos conhecemos o conceito de funções. Resumindo, as funções são
equações matemáticas que produzem uma saída ao fornecer entrada. Por exemplo:
Suponha que a função F(x) seja uma função definida por: F(x) = x^2 4
Podemos escrever o código Java para esta função como:

public static int F(int x){
retornar (x * x 4);
}

Agora, podemos passar diferentes valores de x para esta função e receber nossa saída
de acordo.
Antes de passar para a recursão, vamos tentar entender outra questão matemática
conceito conhecido como Princípio de Indução Matemática (PMI).

Princípio de Indução Matemática (PMI) é uma técnica para provar uma afirmação, uma
fórmula, ou um teorema que é afirmado sobre um conjunto de números naturais. Tem o
seguindo três etapas:
1.** Etapa do caso trivial*: Nesta etapa, provaremos a afirmação desejada para
um caso base como n = 0 ou n = 1.
2.* Etapa de suposição**: Nesta etapa, assumiremos que a afirmação desejada
é válido para n = k.

1. Para provar a etapa: A partir dos resultados da etapa de suposição, provaremos que, n = k 1 também é verdadeiro para a equação desejada sempre que n = k é verdadeiro.

Por exemplo: vamos provar usando o Princípio da Indução Matemática que:
S(N): 1 2 3 ... N = (N * (N 1))/2
(A soma dos primeiros N números naturais)
Prova:
Etapa 1: para N = 1, S(1) = 1 é verdadeiro.
Etapa 2: suponha que a afirmação fornecida seja verdadeira para N = k, ou seja,
1 2 3 .... k = (k * (k 1))/2
Etapa 3: vamos provar a afirmação para N = k 1 usando a etapa 2.

Para provar: 1 2 3 ... (k 1) = ((k 1)*(k 2))/2
Prova:

Adicionando (k 1) a LHS e RHS no resultado obtido na etapa 2:
1 2 3 ... (k 1) = (k*(k 1))/2 (k 1)

Agora, pegando (k 1) comum do lado RHS:
1 2 3 ... (k 1) = (k 1)*((k 2)/2)

De acordo com a afirmação que estamos tentando provar:
1 2 3 ... (k 1) = ((k 1)*(k 2))/2
Daí provado.

Trabalho de recursão

Podemos definir as etapas da abordagem recursiva resumindo as três acima
passos:
● Caso base: uma função recursiva deve ter uma condição de terminação na qual
o processo irá parar de se chamar. Tal caso é conhecido como caso base. Sem um caso base, ele continuará chamando a si mesmo e ficará preso em um
loop infinito. Em breve, a profundidade de recursão* será excedida e lançará
um erro.
● Chamada recursiva: a função recursiva se invocará em uma versão menor
do problema principal. Precisamos ter cuidado ao escrever esta etapa como ela é
crucial para descobrir corretamente qual é o seu problema menor.
● Cálculo pequeno: geralmente, realizamos uma etapa de cálculo em cada recursivo
chamar. Podemos realizar esta etapa de cálculo antes ou depois da chamada recursiva
dependendo da natureza do problema.

Nota: A recursão usa uma pilha integrada que armazena chamadas recursivas. Portanto, o
o número de chamadas recursivas deve ser o menor possível para evitar estouro de memória. Se
o número de chamadas de recursão excede o valor máximo permitido, o
**profundidade de recursão** será excedida.
Agora, vamos ver como resolver alguns problemas comuns usando Recursão

Declaração do problema - Encontre o fatorial de um número

Abordagem: Descobrir as três etapas do PMI e depois relacioná-las usando
recursão

1. Etapa de Indução: Calculando o fatorial de um número n - F(n) Hipótese de Indução: Já obtivemos o fatorial de n-1 - F(n-1)
2. Expressando F(n) em termos de F(n-1): F(n)=n*F(n-1). Assim obtemos

fato interno estático público(int n){
int resposta = fato(n-1); #Etapa de suposição
retornar resposta * n; #Resolvendo problema a partir da etapa de suposição
}

1. O código ainda não está completo. A parte que falta é o caso base. Agora vamos simulação para encontrar o caso em que a recursão precisa parar. Considere n = 5:

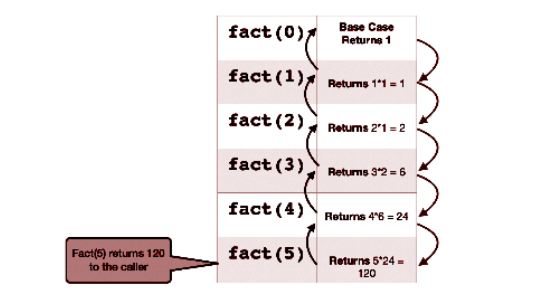
Como podemos ver acima, já sabemos a resposta de n = 0, que é 1. Então vamos
mantenha isso como nosso caso base. Portanto, o código agora se torna:

public static int fatorial(int n){
if (n == 0) // caso base
retornar 1;
outro
retornar n*fatorial(n-1); // caso recursivo
}