k-Regressão dos vizinhos mais próximos

k-Nearest Neighbours (k-NN) é um método não paramétrico que prevê o valor de saída com base na média (ou média ponderada) dos k-pontos de dados de treinamento mais próximos no espaço de recursos. Essa abordagem pode modelar efetivamente relacionamentos complexos em dados sem assumir uma forma funcional específica.

O método de regressão k-NN pode ser resumido da seguinte forma:

1. Métrica de distância: O algoritmo usa uma métrica de distância (geralmente distância euclidiana) para determinar a "proximidade" dos pontos de dados.
2. k Vizinhos: O parâmetro k especifica quantos vizinhos mais próximos devem ser considerados ao fazer previsões.
3. Predição: O valor previsto para um novo ponto de dados é a média dos valores de seus k vizinhos mais próximos.

Conceitos-chave

1. Não paramétrico: Ao contrário dos modelos paramétricos, k-NN não assume uma forma específica para o relacionamento subjacente entre os recursos de entrada e a variável de destino. Isso o torna flexível na captura de padrões complexos.

2. Cálculo de distância: A escolha da métrica de distância pode afetar significativamente o desempenho do modelo. As métricas comuns incluem distâncias euclidianas, de Manhattan e de Minkowski.

3. Escolha de k: O número de vizinhos (k) pode ser escolhido com base na validação cruzada. Um k pequeno pode levar a um ajuste excessivo, enquanto um k grande pode suavizar demais a previsão, potencialmente um ajuste insuficiente.

Exemplo de regressão de k-vizinhos mais próximos

Este exemplo demonstra como usar a regressão k-NN com recursos polinomiais para modelar relacionamentos complexos enquanto aproveita a natureza não paramétrica de k-NN.

Exemplo de código Python

1. Importar bibliotecas

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

Este bloco importa as bibliotecas necessárias para manipulação de dados, plotagem e aprendizado de máquina.

2. Gerar dados de amostra

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

Este bloco gera dados de amostra representando uma relação com algum ruído, simulando variações de dados do mundo real.

3. Divida o conjunto de dados

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Este bloco divide o conjunto de dados em conjuntos de treinamento e teste para avaliação do modelo.

4. Criar recursos polinomiais

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

Este bloco gera recursos polinomiais a partir dos conjuntos de dados de treinamento e teste, permitindo que o modelo capture relacionamentos não lineares.

5. Crie e treine o modelo de regressão k-NN

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

Este bloco inicializa o modelo de regressão k-NN e o treina usando os recursos polinomiais derivados do conjunto de dados de treinamento.

6. Faça previsões

y_pred = knn_model.predict(X_poly_test)

Este bloco usa o modelo treinado para fazer previsões no conjunto de teste.

7. Trace os resultados

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

Este bloco cria um gráfico de dispersão dos pontos de dados reais versus os valores previstos do modelo de regressão k-NN, visualizando a curva ajustada.

Saída com k = 1:

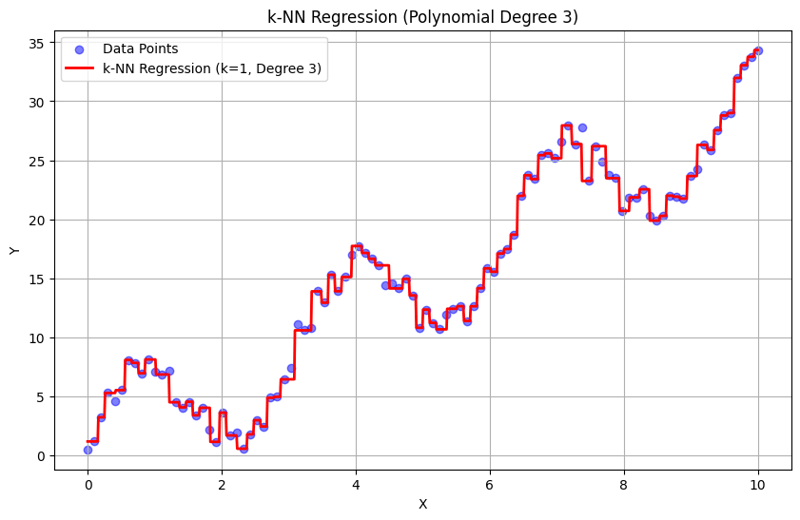
Saída com k = 10:

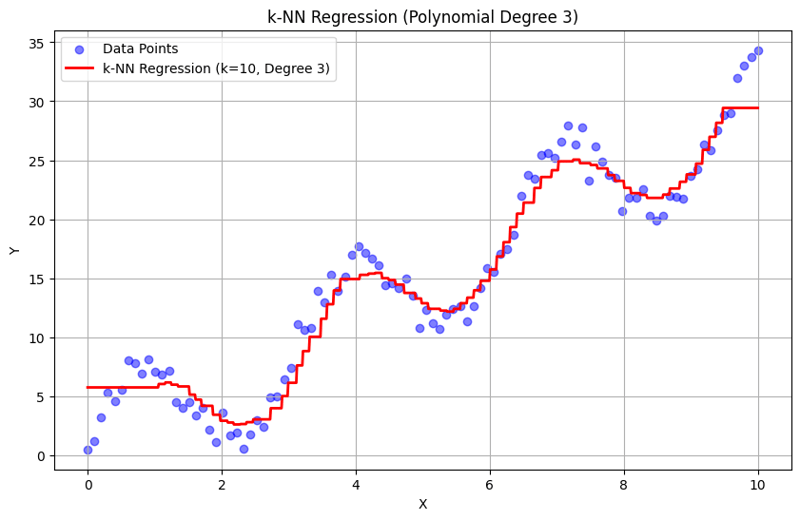
Esta abordagem estruturada demonstra como implementar e avaliar a regressão de k-vizinhos mais próximos com recursos polinomiais. Ao capturar padrões locais por meio da média das respostas de vizinhos próximos, a regressão k-NN modela efetivamente relacionamentos complexos em dados, ao mesmo tempo que fornece uma implementação direta. A escolha do k e do grau polinomial influencia significativamente o desempenho e a flexibilidade do modelo na captura de tendências subjacentes.