Esta seção apresenta algoritmos eficientes para encontrar o par de pontos mais próximo usando divisão e conquista. Dado um conjunto de pontos, o problema do par mais próximo consiste em encontrar os dois pontos mais próximos um do outro. Conforme mostrado na figura abaixo, uma linha é desenhada para conectar os dois pontos mais próximos na animação do par mais próximo.

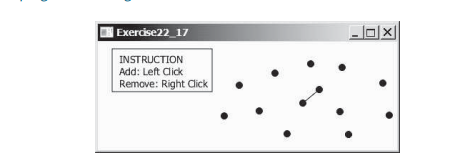
Estudo de caso: Encontrando o par mais próximo, apresentou um algoritmo de força bruta para encontrar o par de pontos mais próximo. O algoritmo calcula as distâncias entre todos os pares de pontos e encontra aquele com a distância mínima. Claramente, o algoritmo leva tempo O (n ^ 2). Podemos projetar um algoritmo mais eficiente?

Usaremos uma abordagem chamada dividir e conquistar para resolver esse problema. A abordagem divide o problema em subproblemas, resolve os subproblemas e depois combina as soluções dos subproblemas para obter a solução para todo o problema. Ao contrário da abordagem de programação dinâmica, os subproblemas da abordagem dividir para conquistar não se sobrepõem. Um subproblema é como o problema original com tamanho menor, então você pode aplicar recursão para resolver o problema. Na verdade, todas as soluções para problemas recursivos seguem a abordagem de dividir para conquistar.

As etapas abaixo descrevem como resolver o problema do par mais próximo usando a abordagem de dividir e conquistar.

• Etapa 1: Classifique os pontos em ordem crescente de coordenadas x. Para os pontos com as mesmas coordenadas x, classifique pelas coordenadas y. Isso resulta em uma lista ordenada S de pontos.
• Etapa 2: Divida S em dois subconjuntos, S1 e S2, de tamanho igual usando o ponto médio na lista classificada. Seja o ponto médio em S1. Encontre recursivamente o par mais próximo em S1 e S2. Sejam d1 e d2 a distância dos pares mais próximos nos dois subconjuntos, respectivamente.
• Etapa 3: Encontre o par mais próximo entre um ponto em S1 e um ponto em S2 e denote sua distância como d3. O par mais próximo é aquele com distância min(d1, d2, d3).

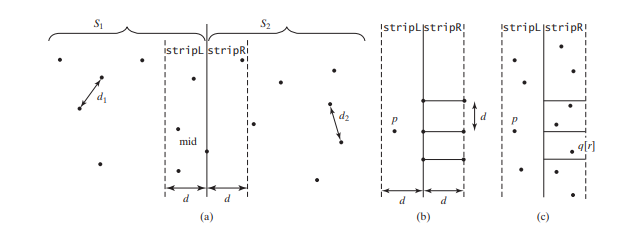
A classificação por seleção leva tempo O(n^2). A etapa 1 pode ser realizada em tempo O (n log n). A etapa 3 pode ser realizada em tempo O(n). Seja d = min(d1, d2). Já sabemos que a distância do par mais próximo não pode ser maior que d. Para que um ponto em S1 e um ponto em S2 formem o par mais próximo em S, o ponto esquerdo deve estar em stripL e o ponto direito em stripR, conforme ilustrado na Figura abaixo ( a).

Para um ponto p em stripL, basta considerar um ponto reto dentro do retângulo d X 2d, conforme mostrado em (b) abaixo. Qualquer ponto certo fora do retângulo não pode formar o par mais próximo de p. Como a distância do par mais próximo em S2 é maior ou igual a d, pode haver no máximo seis
pontos no retângulo. Assim, para cada ponto em stripL, no máximo seis pontos em stripR precisam ser considerados.

Para cada ponto p em stripL, como você localiza os pontos na área do retângulo d X 2d correspondente em stripR? Isso pode ser feito de forma eficiente se os pontos em stripL e stripR forem classificados em ordem crescente de suas coordenadas y. Seja pointsOrderedOnY a lista dos pontos classificados em ordem crescente de coordenadas y. pointsOrderedOnY pode ser obtido antecipadamente no algoritmo. stripL e stripR podem ser obtidos em pointsOrderedOnY na Etapa 3, conforme mostrado no código abaixo.

para cada ponto p em pointsOrderedOnY
if (p está em S1 e mid.x – px acrescente p a stripL;
senão if (p está em S2 e px - mid.x acrescente p a stripR;

Deixe os pontos em stripL e stripR serem {p0, p1, ... , pk} e {q0, q1, ... , qt}, como mostrado em Figura acima (c). O par mais próximo entre um ponto em stripL e um ponto em stripR pode ser encontrado usando o algoritmo descrito no código abaixo.

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



Os pontos em stripL são considerados de p0, p1, ... , pk nesta ordem. Para um ponto p em stripL, pule os pontos em stripR que estão abaixo de p.y – d (linhas 5–6). Quando um ponto for ignorado, ele não será mais considerado. O loop while (linhas 9–17) verifica se (p, q[r1]) é um possível par mais próximo. Existem no máximo seis desses pares q[r1], porque a distância entre dois pontos em stripR não pode ser menor que d. Portanto, a complexidade para encontrar o par mais próximo na Etapa 3 é O(n).

Observe que a Etapa 1 nas etapas acima é executada apenas uma vez para pré-classificar os pontos. Suponha que todos os pontos estejam pré-classificados. Deixe T(n) denotar a complexidade de tempo para este algoritmo. Por isso,



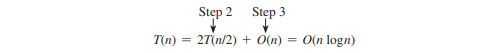
Portanto, o par de pontos mais próximo pode ser encontrado em tempo O(n log n).