Esta seção fornece vários exemplos de determinação do Big O para instruções de repetição, sequência e seleção.

Exemplo 1

Considere a complexidade de tempo para o seguinte loop:

for (int i = 1; i k = k 5;
}

É um tempo constante, c, para execução

k = k 5;

Como o loop é executado n vezes, a complexidade de tempo do loop é

T(n) = (uma constante c)*n = O(n).

A análise teórica prevê o desempenho do algoritmo. Para ver o desempenho desse algoritmo, executamos o código no programa abaixo para obter o tempo de execução para n = 1000000, 10000000, 100000000 e 100000000.

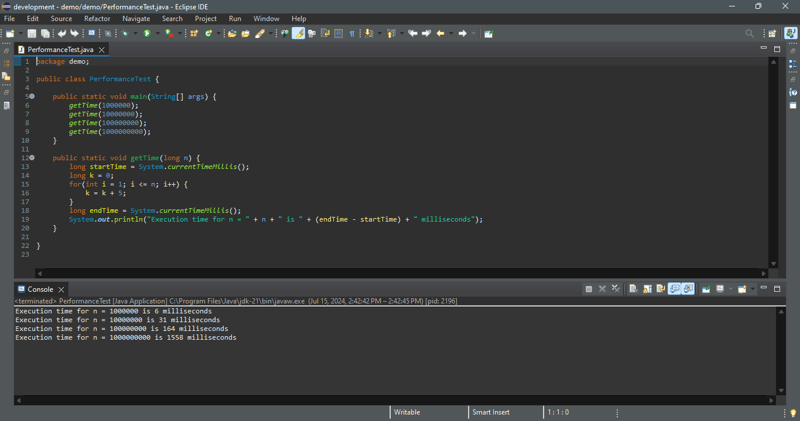
Nossa análise prevê uma complexidade de tempo linear para este loop. Conforme mostrado no exemplo de saída, quando o tamanho da entrada aumenta 10 vezes, o tempo de execução aumenta aproximadamente 10 vezes. A execução confirma a previsão.

Exemplo 2

Qual é a complexidade de tempo para o loop a seguir?

for (int i = 1; i para (int j = 1; j k = k eu j;
}
}

É um tempo constante, c, para execução

k = k i j;

O loop externo é executado n vezes. Para cada iteração no loop externo, o loop interno é executado n vezes. Assim, a complexidade de tempo do loop é

T(n) = (uma constante c)*n*n = O(n^2)

Um algoritmo com complexidade de tempo O(n^2) é chamado de algoritmo quadrático e exibe uma taxa de crescimento quadrática. O algoritmo quadrático cresce rapidamente à medida que o tamanho do problema aumenta. Se você dobrar o tamanho da entrada, o tempo do algoritmo será quadruplicado. Algoritmos com um loop aninhado geralmente são quadráticos.

Exemplo 3

Considere o seguinte ciclo:

for (int i = 1; i para (int j = 1; j k = k eu j;
}
}

O loop externo é executado n vezes. Para i = 1, 2, c , o loop interno é executado uma vez, duas vezes e n vezes. Assim, a complexidade de tempo do loop é

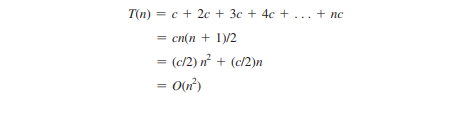
Exemplo 4

Considere o seguinte ciclo:

for (int i = 1; i para (int j = 1; j k = k eu j;
}
}

O loop interno é executado 20 vezes e o loop externo n vezes. Portanto, a complexidade de tempo do loop é

T(n) = 20*c*n = O(n)

Exemplo 5

Considere as seguintes sequências:

para (int j = 1; j k = k4;
}

for (int i = 1; i para (int j = 1; j k = k eu j;
}
}

O primeiro loop é executado 10 vezes e o segundo loop 20 * n vezes. Assim, a complexidade de tempo do loop é

T(n) = 10*c 20*c*n = O(n)

Exemplo 6

Considere a seguinte declaração de seleção:

if (lista.contém(e)) {
System.out.println(e);
}
outro
para (Objeto t: lista) {
System.out.println(t);
}

Suponha que a lista contenha n elementos. O tempo de execução para list.contains(e) é O(n). O loop na cláusula else leva tempo O(n). Portanto, a complexidade de tempo para toda a instrução é

Exemplo 7

Considere o cálculo de a^n para um número inteiro n. Um algoritmo simples multiplicaria n vezes, como segue:

resultado = 1;
para (int i = 1; i resultado *= uma;

O algoritmo leva O(n) tempo. Sem perda de generalidade, assuma n = 2^k. Você pode melhorar o algoritmo usando o seguinte esquema:

resultado = a;
para (int i = 1; i resultado = resultado * resultado;

O algoritmo leva tempo O(logn). Para um n arbitrário, você pode revisar o algoritmo e provar que a complexidade ainda é O(logn).

Para simplificar, como 0(logn) = 0(log2n) = 0(logan), a base constante é omitida.