Projeto de algoritmo é desenvolver um processo matemático para resolver um problema. A análise de algoritmo visa prever o desempenho de um algoritmo. Os dois capítulos anteriores introduziram estruturas de dados clássicas (listas, pilhas, filas, filas de prioridade, conjuntos e mapas) e as aplicaram para resolver problemas. Este capítulo usará uma variedade de exemplos para apresentar técnicas algorítmicas comuns (programação dinâmica, divisão e conquista e retrocesso) para o desenvolvimento de algoritmos eficientes.

A notação Big O obtém uma função para medir a complexidade do tempo do algoritmo com base no tamanho da entrada. Você pode ignorar constantes multiplicativas e termos não dominantes na função. Suponha que dois algoritmos executem a mesma tarefa, como pesquisa (pesquisa linear vs. pesquisa binária). Qual é o melhor? Para responder a esta pergunta, você pode implementar esses algoritmos e executar os programas para obter o tempo de execução. Mas há dois problemas com esta abordagem:

• Primeiro, muitas tarefas são executadas simultaneamente em um computador. O tempo de execução de um determinado programa depende da carga do sistema.
• Em segundo lugar, o tempo de execução depende da entrada específica. Considere, por exemplo, pesquisa linear e pesquisa binária. Se um elemento a ser pesquisado for o primeiro na lista, a pesquisa linear encontrará o elemento mais rapidamente do que a pesquisa binária.

É muito difícil comparar algoritmos medindo seu tempo de execução. Para superar esses problemas, foi desenvolvida uma abordagem teórica para analisar algoritmos independentes de computadores e entradas específicas. Esta abordagem aproxima o efeito de uma mudança no tamanho da entrada. Dessa forma, você pode ver quão rápido o tempo de execução de um algoritmo aumenta à medida que o tamanho da entrada aumenta, para que você possa comparar dois algoritmos examinando suas taxas de crescimento.

Considere a pesquisa linear. O algoritmo de pesquisa linear compara a chave com os elementos da matriz sequencialmente até que a chave seja encontrada ou a matriz se esgote. Se a chave não estiver na matriz, serão necessárias comparações n para uma matriz de tamanho n. Se a chave estiver na matriz, serão necessárias n/2 comparações em média. O tempo de execução do algoritmo é proporcional ao tamanho do array. Se você dobrar o tamanho do array, espera-se que o número de comparações dobre. O algoritmo cresce a uma taxa linear. A taxa de crescimento tem uma ordem de grandeza de n. Os cientistas da computação usam a notação Big O para representar a “ordem de magnitude”. Usando esta notação, a complexidade do algoritmo de pesquisa linear é O(n), pronunciada como “ordem de n.” Chamamos um algoritmo com complexidade de tempo O(n) de algoritmo linear e ele exibe uma taxa de crescimento linear.

Para o mesmo tamanho de entrada, o tempo de execução de um algoritmo pode variar, dependendo da entrada. Uma entrada que resulta no tempo de execução mais curto é chamada de entrada de melhor caso, e uma entrada que resulta no tempo de execução mais longo é chamada de entrada de pior caso. Análise do melhor caso e
a análise do pior caso consiste em analisar os algoritmos quanto à entrada do melhor e do pior caso. As análises do melhor e do pior caso não são representativas, mas a análise do pior caso é muito útil. Você pode ter certeza de que o algoritmo nunca será mais lento do que o pior caso.
Uma análise de caso médio tenta determinar a quantidade média de tempo entre todas as entradas possíveis do mesmo tamanho. A análise do caso médio é ideal, mas difícil de executar, porque para muitos problemas é difícil determinar as probabilidades relativas e as distribuições de várias instâncias de entrada. A análise do pior caso é mais fácil de realizar, portanto a análise geralmente é conduzida para o pior caso.

O algoritmo de pesquisa linear requer comparações n no pior caso e comparações n/2 no caso médio se você estiver quase sempre procurando por algo conhecido por estar na lista. Usando a notação Big O, ambos os casos requerem tempo O(n). A constante multiplicativa (1/2) pode ser omitida. A análise do algoritmo está focada na taxa de crescimento. As constantes multiplicativas não têm impacto nas taxas de crescimento. A taxa de crescimento para n/2 ou 100_n_ é a mesma que para n, conforme ilustrado na tabela abaixo, Taxas de crescimento. Portanto, O(n) = O(n/2) = O(100n).

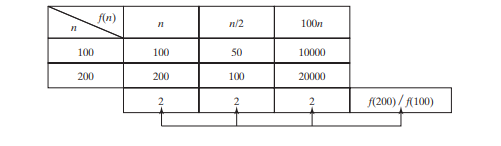
Considere o algoritmo para encontrar o número máximo em uma matriz de n elementos. Para encontrar o número máximo se n for 2, é necessária uma comparação; se n for 3, duas comparações. Em geral, são necessárias n - 1 comparações para encontrar o número máximo em uma lista de n elementos. A análise de algoritmo é para grandes tamanhos de entrada. Se o tamanho da entrada for pequeno, não há significância na estimativa da eficiência de um algoritmo. À medida que n aumenta, a parte n da expressão n - 1 domina a complexidade. A notação Big O permite ignorar a parte não dominante (por exemplo, -1 no
expressão n - 1) e destaque a parte importante (por exemplo, n na expressão n - 1). Portanto, a complexidade deste algoritmo é O(n).

A notação Big O estima o tempo de execução de um algoritmo em relação ao tamanho da entrada. Se o tempo não estiver relacionado ao tamanho da entrada, diz-se que o algoritmo leva tempo constante com a notação O(1). Por exemplo, um método que recupera um elemento em um determinado índice em um array
leva um tempo constante, porque o tempo não aumenta à medida que o tamanho da matriz aumenta.

Os seguintes somatórios matemáticos são frequentemente úteis na análise de algoritmos:

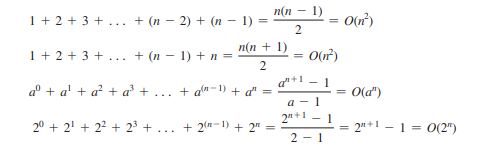
Complexidade de tempo é uma medida do tempo de execução usando a notação Big-O. Da mesma forma, você também pode medir complexidade espacial usando a notação Big-O. Complexidade do espaço mede a quantidade de espaço de memória usado por um algoritmo. A complexidade do espaço para a maioria dos algoritmos apresentados no livro é O(n). ou seja, eles exibem taxa de crescimento linear para o tamanho da entrada. Por exemplo, a complexidade do espaço para pesquisa linear é O(n).