The WeightedGraph class extends AbstractGraph.
The preceding chapter designed the Graph interface, the AbstractGraph class, and the UnweightedGraph class for modeling graphs. Following this pattern, we design WeightedGraph as a subclass of AbstractGraph, as shown in Figure below.

WeightedGraph simply extends AbstractGraph with five constructors for creating concrete WeightedGraph instances. WeightedGraph inherits all methods from AbstractGraph, overrides the clear and addVertex methods, implements a new addEdge method for adding a weighted edge, and also introduces new methods for obtaining minimum spanning trees and for finding all single-source shortest paths. Minimum spanning trees and shortest paths will be introduced in Sections Minimum spanning trees and shortest paths, respectively.

The code below implements WeightedGraph. Edge adjacency lists (lines 38–63) are used internally to store adjacent edges for a vertex. When a WeightedGraph is constructed, its edge adjacency lists are created (lines 47 and 57). The methods getMinimumSpanningTree() (lines 99–138) and getShortestPath() (lines 156–197) will be introduced in upcoming sections.

package demo;
import java.util.*;

public class WeightedGraph extends AbstractGraph {
    /** Construct an empty */
    public WeightedGraph() {}

    /** Construct a WeightedGraph from vertices and edged in arrays */
    public WeightedGraph(V[] vertices, int[][] edges) {
        createWeightedGraph(java.util.Arrays.asList(vertices), edges);
    }

     /** Construct a WeightedGraph from vertices and edges in list */
    public WeightedGraph(int[][] edges, int numberOfVertices) {
        List vertices = new ArrayList();
        for (int i = 0; i  vertices, List edges) {
        createWeightedGraph(vertices, edges);
    }

    /** Construct a WeightedGraph from vertices 0, 1, and edge array */
    public WeightedGraph(List edges, int numberOfVertices) {
        List vertices = new ArrayList();
        for (int i = 0; i  vertices, int[][] edges) {
        this.vertices = vertices;

        for (int i = 0; i ()); // Create a list for vertices
        }

        for (int i = 0; i  vertices, List edges) {
        this.vertices = vertices;

        for (int i = 0; i ()); // Create a list for vertices
        }

        for (WeightedEdge edge: edges) {
            neighbors.get(edge.u).add(edge); // Add an edge into the list
        }
    }

    /** Return the weight on the edge (u, v) */
    public double getWeight(int u, int v) throws Exception {
        for (Edge edge : neighbors.get(u)) {
            if (edge.v == v) {
                return ((WeightedEdge)edge).weight;
            }
        }

        throw new Exception("Edge does not exit");
    }

    /** Display edges with weights */
    public void printWeightedEdges() {
        for (int i = 0; i  T = new ArrayList();

        // Expand T
        while (T.size()  ((WeightedEdge)e).weight) {
                    cost[e.v] = ((WeightedEdge)e).weight;
                    parent[e.v] = u;
                }
            }
        } // End of while

        return new MST(startingVertex, parent, T, totalWeight);
    }

    /** MST is an inner class in WeightedGraph */
    public class MST extends Tree {
        private double totalWeight; // Total weight of all edges in the tree

        public MST(int root, int[] parent, List searchOrder, double totalWeight) {
            super(root, parent, searchOrder);
            this.totalWeight = totalWeight;
        }

        public double getTotalWeight() {
            return totalWeight;
        }
    }

    /** Find single source shortest paths */
    public ShortestPathTree getShortestPath(int sourceVertex) {
        // cost[v] stores the cost of the path from v to the source
        double[] cost = new double[getSize()];
        for (int i = 0; i  T = new ArrayList();

        // Expand T
        while (T.size()  cost[u]   ((WeightedEdge)e).weight) {
                    cost[e.v] = cost[u]   ((WeightedEdge)e).weight;
                    parent[e.v] = u;
                }
            }
        } // End of while

        // Create a ShortestPathTree
        return new ShortestPathTree(sourceVertex, parent, T, cost);
    }

    /** ShortestPathTree is an inner class in WeightedGraph */
    public class ShortestPathTree extends Tree {
        private double[] cost; // cost[v] is the cost from v to source

        /** Construct a path */
        public ShortestPathTree(int source, int[] parent, List searchOrder, double[] cost) {
            super(source, parent, searchOrder);
            this.cost = cost;
        }

        /** Return the cost for a path from the root to vertex v */
        public double getCost(int v) {
            return cost[v];
        }

        /** Print paths from all vertices to the source */
        public void printAllPaths() {
            System.out.println("All shortest paths from "   vertices.get(getRoot())   " are:");
            for (int i = 0; i 



The WeightedGraph class extends the AbstractGraph class (line 3). The properties vertices and neighbors in AbstractGraph are inherited in WeightedGraph.neighbors is a list. Each element is the list is another list that contains edges. For unweighted graph, each edge is an instance of AbstractGraph.Edge. For a weighted graph, each edge is an instance of WeightedEdge. WeightedEdge is a subtype of Edge. So you can add a weighted edge into neighbors.get(i) for a weighted graph (line 47).

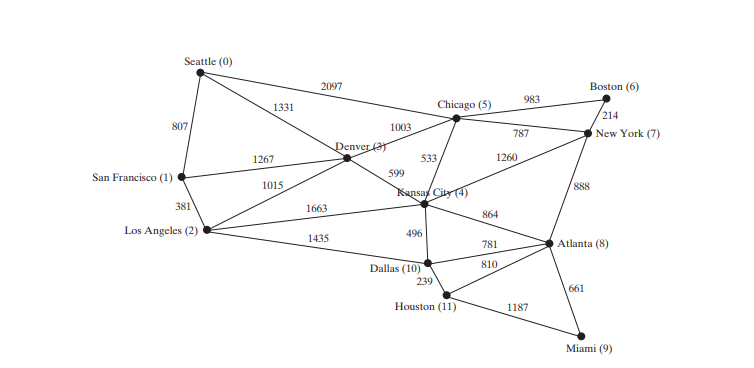
The code below gives a test program that creates a graph for the one in Figure below and another graph for the one in Figure below a.






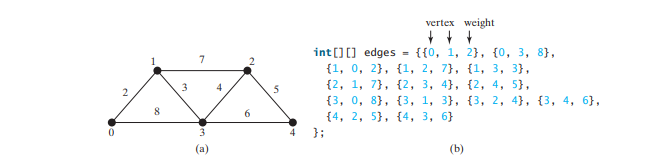
package demo;

public class TestWeightedGraph {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1, 807}, {0, 3, 1331}, {0, 5, 2097},
                {1, 0, 807}, {1, 2, 381}, {1, 3, 1267},
                {2, 1, 381}, {2, 3, 1015}, {2, 4, 1663}, {2, 10, 1435},
                {3, 0, 1331}, {3, 1, 1267}, {3, 2, 1015}, {3, 4, 599}, {3, 5, 1003},
                {4, 2, 1663}, {4, 3, 599}, {4, 5, 533}, {4, 7, 1260}, {4, 8, 864}, {4, 10, 496},
                {5, 0, 2097}, {5, 3, 1003}, {5, 4, 533}, {5, 6, 983}, {5, 7, 787},
                {6, 5, 983}, {6, 7, 214},
                {7, 4, 1260}, {7, 5, 787}, {7, 6, 214}, {7, 8, 888},
                {8, 4, 864}, {8, 7, 888}, {8, 9, 661}, {8, 10, 781}, {8, 11, 810},
                {9, 8, 661}, {9, 11, 1187},
                {10, 2, 1435}, {10, 4, 496}, {10, 8, 781}, {10, 11, 239},
                {11, 8, 810}, {11, 9, 1187}, {11, 10, 239}
        };

        WeightedGraph graph1 = new WeightedGraph(vertices, edges);
        System.out.println("The number of vertices in graph1: "   graph1.getSize());
        System.out.println("The vertex with index 1 is "   graph1.getVertex(1));
        System.out.println("The index for Miami is "   graph1.getIndex("Miami"));
        System.out.println("The edges for graph1:");
        graph1.printWeightedEdges();

        edges = new int[][] {
            {0, 1, 2}, {0, 3, 8},
            {1, 0, 2}, {1, 2, 7}, {1, 3, 3},
            {2, 1, 7}, {2, 3, 4}, {2, 4, 5},
            {3, 0, 8}, {3, 1, 3}, {3, 2, 4}, {3, 4, 6},
            {4, 2, 5}, {4, 3, 6}
        };
        WeightedGraph graph2 = new WeightedGraph(edges, 5);
        System.out.println("\nThe edges for graph2:");
        graph2.printWeightedEdges();
    }
}





The number of vertices in graph1: 12

The vertex with index 1 is San Francisco

The index for Miami is 9

The edges for graph1:

Vertex 0: (0, 1, 807) (0, 3, 1331) (0, 5, 2097)

Vertex 1: (1, 2, 381) (1, 0, 807) (1, 3, 1267)

Vertex 2: (2, 1, 381) (2, 3, 1015) (2, 4, 1663) (2, 10, 1435)

Vertex 3: (3, 4, 599) (3, 5, 1003) (3, 1, 1267)

 (3, 0, 1331) (3, 2, 1015)

Vertex 4: (4, 10, 496) (4, 8, 864) (4, 5, 533) (4, 2, 1663)

 (4, 7, 1260) (4, 3, 599)

Vertex 5: (5, 4, 533) (5, 7, 787) (5, 3, 1003)

 (5, 0, 2097) (5, 6, 983)

Vertex 6: (6, 7, 214) (6, 5, 983)

Vertex 7: (7, 6, 214) (7, 8, 888) (7, 5, 787) (7, 4, 1260)

Vertex 8: (8, 9, 661) (8, 10, 781) (8, 4, 864)

 (8, 7, 888) (8, 11, 810)

Vertex 9: (9, 8, 661) (9, 11, 1187)

Vertex 10: (10, 11, 239) (10, 4, 496) (10, 8, 781) (10, 2, 1435)

Vertex 11: (11, 10, 239) (11, 9, 1187) (11, 8, 810)

The edges for graph2:

Vertex 0: (0, 1, 2) (0, 3, 8)

Vertex 1: (1, 0, 2) (1, 2, 7) (1, 3, 3)

Vertex 2: (2, 3, 4) (2, 1, 7) (2, 4, 5)

Vertex 3: (3, 1, 3) (3, 4, 6) (3, 2, 4) (3, 0, 8)

Vertex 4: (4, 2, 5) (4, 3, 6)

The program creates graph1 for the graph in Figure above in lines 3–27. The vertices for graph1 are defined in lines 3–5. The edges for graph1 are defined in lines 7–24. The edges are represented using a two-dimensional array. For each row i in the array, edges[i][0] and edges[i][1] indicate that there is an edge from vertex edges[i][0] to vertex edges[i][1] and the weight for the edge is edges[i][2]. For example, {0, 1, 807} (line 8) represents the edge from vertex 0 (edges[0][0]) to vertex 1 (edges[0][1]) with weight 807 (edges[0][2]). {0, 5, 2097} (line 8) represents the edge from vertex 0 (edges[2][0]) to vertex 5 (edges[2][1]) with weight 2097 (edges[2][2]). Line 35 invokes the printWeightedEdges() method on graph1 to display all edges in graph1.

The program creates the edges for graph2 for the graph in Figure above a in lines 37–44. Line 46 invokes the printWeightedEdges() method on graph2 to display all edges in graph2.