k-최근접이웃 회귀

k-NN(k-Nearest Neighbors) 회귀는 특징 공간에서 k-최근접 학습 데이터 포인트의 평균(또는 가중 평균)을 기반으로 출력 값을 예측하는 비모수적 방법입니다. 이 접근 방식은 특정 기능적 형태를 가정하지 않고도 데이터의 복잡한 관계를 효과적으로 모델링할 수 있습니다.

k-NN 회귀 방법은 다음과 같이 요약할 수 있습니다.

1. 거리 측정법: 알고리즘은 거리 측정법(일반적으로 유클리드 거리)을 사용하여 데이터 포인트의 "가까움"을 결정합니다.
2. k 이웃: 매개변수 k는 예측 시 고려해야 할 가장 가까운 이웃 수를 지정합니다.
3. 예측: 새 데이터 포인트에 대한 예측 값은 k개의 최근접 이웃 값의 평균입니다.

주요 개념

1. 비모수적: 매개변수적 모델과 달리 k-NN은 입력 특성과 대상 변수 간의 기본 관계에 대해 특정 형식을 가정하지 않습니다. 이를 통해 복잡한 패턴을 유연하게 캡처할 수 있습니다.

2. 거리 계산: 거리 측정법의 선택은 모델 성능에 큰 영향을 미칠 수 있습니다. 일반적인 측정항목에는 유클리드, 맨해튼, 민코프스키 거리가 포함됩니다.

3. k 선택: 교차 검증을 기반으로 이웃 수(k)를 선택할 수 있습니다. k가 작으면 과적합이 발생할 수 있고, k가 크면 예측이 너무 평활화되어 잠재적으로 과소적합이 발생할 수 있습니다.

k-최근접이웃 회귀 예제

이 예에서는 k-NN의 비모수적 특성을 활용하면서 다항식 기능이 포함된 k-NN 회귀를 사용하여 복잡한 관계를 모델링하는 방법을 보여줍니다.

Python 코드 예

1. 라이브러리 가져오기

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

이 블록은 데이터 조작, 플로팅 및 기계 학습에 필요한 라이브러리를 가져옵니다.

2. 샘플 데이터 생성

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

이 블록은 실제 데이터 변형을 시뮬레이션하여 일부 노이즈와의 관계를 나타내는 샘플 데이터를 생성합니다.

3. 데이터세트 분할

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

이 블록은 모델 평가를 위해 데이터 세트를 훈련 세트와 테스트 세트로 분할합니다.

4. 다항식 특징 생성

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

이 블록은 교육 및 테스트 데이터 세트에서 다항식 기능을 생성하여 모델이 비선형 관계를 캡처할 수 있도록 합니다.

5. k-NN 회귀 모델 생성 및 훈련

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

이 블록은 k-NN 회귀 모델을 초기화하고 훈련 데이터 세트에서 파생된 다항식 기능을 사용하여 훈련합니다.

6. 예측하기

y_pred = knn_model.predict(X_poly_test)

이 블록은 훈련된 모델을 사용하여 테스트 세트에 대해 예측합니다.

7. 결과 플롯

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

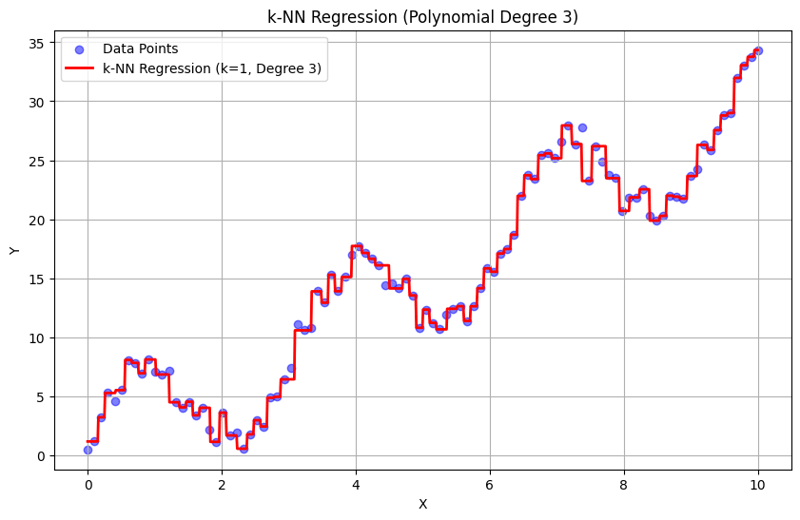
이 블록은 k-NN 회귀 모델의 예측 값과 실제 데이터 포인트의 산점도를 생성하여 적합 곡선을 시각화합니다.

k = 1인 출력:

k = 10인 출력:

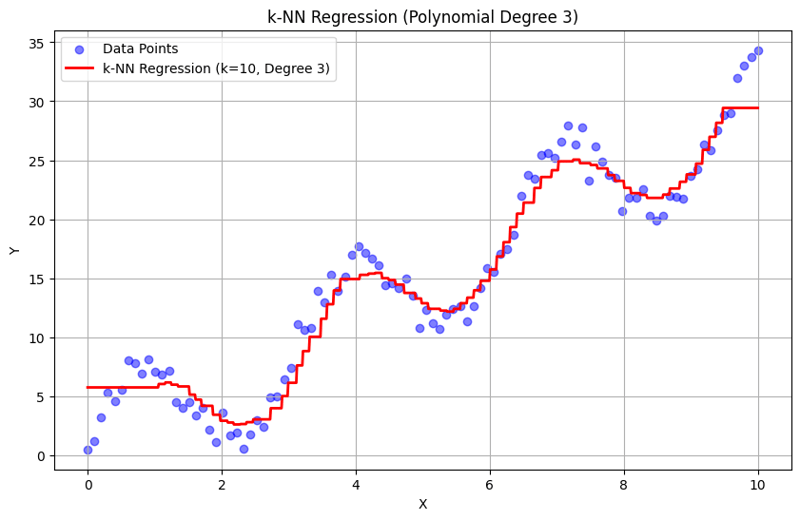
이 구조화된 접근 방식은 다항식 기능을 사용하여 k-최근접 이웃 회귀를 구현하고 평가하는 방법을 보여줍니다. k-NN 회귀는 인근 이웃의 응답 평균을 통해 로컬 패턴을 캡처함으로써 데이터의 복잡한 관계를 효과적으로 모델링하는 동시에 간단한 구현을 제공합니다. k와 다항식 차수의 선택은 모델의 성능과 기본 추세를 포착하는 유연성에 큰 영향을 미칩니다.