그래프 알고리즘을 사용하면 많은 실제 문제를 해결할 수 있습니다. 그래프는 실제 문제를 모델링하고 해결하는 데 유용합니다. 예를 들어, 두 도시 사이의 최소 항공편 수를 찾는 문제는 아래 그림과 같이 정점이 도시를 나타내고 가장자리가 인접한 두 도시 사이의 항공편을 나타내는 그래프를 사용하여 모델링할 수 있습니다. 최소 연결 항공편 수를 찾는 문제
두 도시 사이의 경로는 그래프의 두 꼭지점 사이의 최단 경로를 찾는 것으로 축소됩니다.

그래프 문제에 대한 연구는 그래프 이론으로 알려져 있습니다. 그래프 이론은 1736년 Leonhard Euler가 유명한 쾨니히스베르크의 7개 다리 문제를 풀기 위해 그래프 용어를 도입하면서 창시되었습니다. 프로이센의 쾨니히스베르크 시(현재의 러시아 칼리닌그라드)는 프레겔 강을 경계로 나누어졌습니다. 강에는 두 개의 섬이 있었습니다. 도시와 섬은 아래 그림(a)와 같이 7개의 다리로 연결되어 있다. 문제는 산책을 하고 각 다리를 정확히 한 번씩 건너고 출발점으로 돌아올 수 있느냐는 것이다. 오일러는 그것이 불가능하다는 것을 증명했습니다.

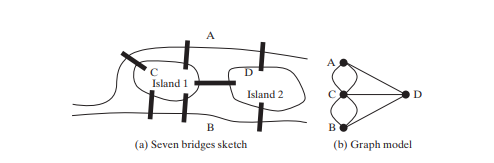
증거를 확립하기 위해 오일러는 먼저 모든 거리를 제거하여 Königsberg 도시 지도를 추상화하고 위 그림(a)에 표시된 스케치를 생성했습니다. 다음으로, 그는 각 땅 덩어리를 꼭지점 또는 노드라고 하는 점으로 바꾸고 각 다리를 가장자리라고 하는 선으로 대체했습니다. 위의 그림 (b). 정점과 가장자리가 있는 이 구조를 그래프라고 합니다.

그래프를 보면 임의의 정점에서 시작하여 모든 가장자리를 정확히 한 번 통과하고 시작 정점으로 돌아가는 경로가 있는지 묻습니다. 오일러는 이러한 경로가 존재하려면 각 꼭지점에 짝수의 변이 있어야 함을 증명했습니다. 따라서 쾨니히스베르크의 7개 다리 문제에는 해결책이 없습니다.

그래프 문제는 종종 알고리즘을 사용하여 해결됩니다. 그래프 알고리즘은 컴퓨터 과학, 수학, 생물학, 공학, 경제, 유전학, 사회 과학 등 다양한 분야에서 다양하게 응용됩니다.

기본 그래프 용어

그래프는 정점과 정점을 연결하는 간선으로 구성됩니다. 이 장에서는 그래프 이론이나 이산 수학에 대한 사전 지식이 있다고 가정하지 않습니다. 우리는 그래프를 정의하기 위해 평범하고 간단한 용어를 사용합니다.

그래프란 무엇인가요? 그래프는 현실 세계의 개체 간의 관계를 나타내는 수학적 구조입니다. 예를 들어, 위 그림의 그래프는 도시 간 비행을 나타내고, 아래 그림 (b)의 그래프는 육지 간 교량을 나타냅니다.

그래프는 비어 있지 않은 정점 집합(노드 또는 점이라고도 함)과 정점을 연결하는 간선 집합으로 구성됩니다. 편의상 그래프를 G = (V, E)로 정의합니다. 여기서 V는 정점 집합을 나타내고 E는 가장자리 집합을 나타냅니다. 예를 들어 아래 그림의 그래프에서 V와 E는 다음과 같습니다.

V = {"시애틀", "샌프란시스코", "로스앤젤레스",
'덴버', '캔자스시티', '시카고', '보스턴', '뉴욕',
'애틀랜타', '마이애미', '댈러스', '휴스턴'};

E = {{"시애틀", "샌프란시스코"},{"시애틀", "시카고"},
{"시애틀", "덴버"}, {"샌프란시스코", "덴버"},
...
};

그래프는 방향이 있을 수도 있고 방향이 없을 수도 있습니다. 유향 그래프에서 각 모서리에는 방향이 있습니다. 이는 모서리를 통해 한 꼭지점에서 다른 꼭지점으로 이동할 수 있음을 나타냅니다. 방향성 그래프를 사용하여 상위/하위 관계를 모델링할 수 있습니다. 정점 A에서 B까지의 간선은 A가 B의 상위임을 나타냅니다. 아래 그림(a)는 방향성 그래프를 보여줍니다.

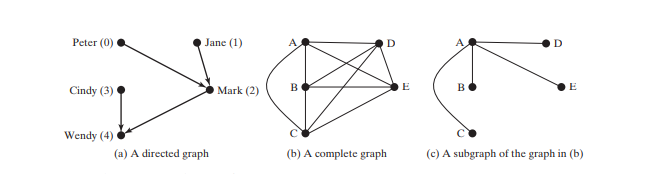
무방향 그래프에서는 정점 사이에서 양방향으로 이동할 수 있습니다. 아래 그림의 그래프는 무방향 그래프입니다.

가장자리에는 가중치가 부여되거나 가중치가 적용되지 않을 수 있습니다. 예를 들어, 위 그림의 그래프에서 각 간선에 가중치를 할당하여 두 도시 사이의 비행 시간을 나타낼 수 있습니다.

그래프의 두 정점이 동일한 가장자리로 연결되어 있으면 인접하다고 합니다. 마찬가지로 두 모서리가 동일한 꼭지점에 연결되어 있으면 인접하다고 합니다. 두 정점을 연결하는 그래프의 간선은 두 정점 모두에 사고라고 합니다. 정점의 차수는 정점에 입사하는 모서리의 수입니다.

두 정점이 인접해 있으면 이웃이라고 합니다. 마찬가지로 두 모서리가 인접해 있으면 이웃이라고 합니다.

루프는 정점을 자신에게 연결하는 가장자리입니다. 두 정점이 두 개 이상의 가장자리로 연결된 경우 이러한 가장자리를 평행 가장자리라고 합니다. 간단한 그래프는 루프나 평행 모서리가 없는 그래프입니다. 완전한 그래프에서는 아래 그림 (b)와 같이 두 쌍의 꼭짓점이 모두 연결되어 있습니다.

그래프의 두 정점 사이에 경로가 있으면 그래프는 연결됩니다. 그래프 G의 하위 그래프는 꼭지점 집합이 G의 부분 집합이고 간선 집합이 G의 부분 집합인 그래프입니다. 예를 들어 위 그림 (c)의 그래프는 위 그림 (b)의 그래프 하위 그래프.

그래프가 연결되어 있고 방향이 지정되지 않았다고 가정합니다. 주기는 정점에서 시작하여 동일한 정점에서 끝나는 닫힌 경로입니다. 연결된 그래프는 순환이 없는 경우 트리입니다. 그래프 G의 스패닝 트리는 G의 연결된 하위 그래프이고 하위 그래프는 G의 모든 정점을 포함하는 트리입니다.