소개

이 기사에서는 Scikit-Learn을 사용한 완전한 머신러닝 프로젝트 워크플로를 시연합니다. 우리는 중위 소득, 주택 연령, 평균 방 수 등 다양한 특성을 기반으로 캘리포니아 주택 가격을 예측하는 모델을 구축할 것입니다. 이 프로젝트는 데이터 로딩, 탐색, 모델 훈련, 평가, 결과 시각화를 포함한 프로세스의 각 단계를 안내합니다. 기본 사항을 이해하려는 초보자이든, 다시 한 번 복습하려는 숙련된 실무자이든, 이 문서는 머신러닝 기술의 실제 적용에 대한 귀중한 통찰력을 제공할 것입니다.

캘리포니아 주택 가격 예측 프로젝트

1. 소개

캘리포니아 주택 시장은 독특한 특성과 가격 역학으로 유명합니다. 본 프로젝트에서는 다양한 특성을 기반으로 주택 가격을 예측하는 머신러닝 모델을 개발하는 것을 목표로 합니다. 우리는 중위 소득, 주택 연령, 평균 방 등과 같은 다양한 속성을 포함하는 캘리포니아 주택 데이터세트를 사용할 것입니다.

2. 라이브러리 가져오기

이 섹션에서는 데이터 조작, 시각화 및 기계 학습 모델 구축에 필요한 라이브러리를 가져옵니다.

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.datasets import fetch_california_housing

3. 데이터세트 로드

캘리포니아 주택 데이터세트를 로드하고 데이터를 구성하기 위해 DataFrame을 생성하겠습니다. 새로운 컬럼으로 목표변수인 주택가격이 추가됩니다.

# Load the California Housing dataset
california = fetch_california_housing()
df = pd.DataFrame(california.data, columns=california.feature_names)
df['PRICE'] = california.target

4. 무작위로 샘플 선택

분석을 관리 가능하게 유지하기 위해 연구 데이터 세트에서 무작위로 700개의 샘플을 선택합니다.

# Randomly Selecting 700 Samples
df_sample = df.sample(n=700, random_state=42)

5. 데이터 살펴보기

이 섹션에서는 데이터세트의 개요를 제공하고 데이터의 기능과 구조를 이해하기 위해 처음 5개 행을 표시합니다.

# Overview of the data
print("First five rows of the dataset:")
print(df_sample.head())

산출

First five rows of the dataset:
       MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  \
20046  1.6812      25.0  4.192201   1.022284      1392.0  3.877437     36.06   
3024   2.5313      30.0  5.039384   1.193493      1565.0  2.679795     35.14   
15663  3.4801      52.0  3.977155   1.185877      1310.0  1.360332     37.80   
20484  5.7376      17.0  6.163636   1.020202      1705.0  3.444444     34.28   
9814   3.7250      34.0  5.492991   1.028037      1063.0  2.483645     36.62   

       Longitude    PRICE  
20046    -119.01  0.47700  
3024     -119.46  0.45800  
15663    -122.44  5.00001  
20484    -118.72  2.18600  
9814     -121.93  2.78000  

DataFrame 정보 표시

print(df_sample.info())

산출

Index: 700 entries, 20046 to 5350
Data columns (total 9 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   MedInc      700 non-null    float64
 1   HouseAge    700 non-null    float64
 2   AveRooms    700 non-null    float64
 3   AveBedrms   700 non-null    float64
 4   Population  700 non-null    float64
 5   AveOccup    700 non-null    float64
 6   Latitude    700 non-null    float64
 7   Longitude   700 non-null    float64
 8   PRICE       700 non-null    float64
dtypes: float64(9)
memory usage: 54.7 KB

요약 통계 표시

print(df_sample.describe())

산출

           MedInc    HouseAge    AveRooms   AveBedrms   Population  \
count  700.000000  700.000000  700.000000  700.000000   700.000000   
mean     3.937653   28.855714    5.404192    1.079266  1387.422857   
std      2.085831   12.353313    1.848898    0.236318  1027.873659   
min      0.852700    2.000000    2.096692    0.500000     8.000000   
25%      2.576350   18.000000    4.397751    1.005934   781.000000   
50%      3.480000   30.000000    5.145295    1.047086  1159.500000   
75%      4.794625   37.000000    6.098061    1.098656  1666.500000   
max     15.000100   52.000000   36.075472    5.273585  8652.000000   

         AveOccup    Latitude   Longitude       PRICE  
count  700.000000  700.000000  700.000000  700.000000  
mean     2.939913   35.498243 -119.439729    2.082073  
std      0.745525    2.123689    1.956998    1.157855  
min      1.312994   32.590000 -124.150000    0.458000  
25%      2.457560   33.930000 -121.497500    1.218500  
50%      2.834524   34.190000 -118.420000    1.799000  
75%      3.326869   37.592500 -118.007500    2.665500  
max      7.200000   41.790000 -114.590000    5.000010  

6. 데이터 세트를 학습 세트와 테스트 세트로 분할

데이터세트를 특성(X)과 대상 변수(y)로 분리한 다음 모델 훈련 및 평가를 위해 훈련 및 테스트 세트로 분할합니다.

# Splitting the dataset into Train and Test sets
X = df_sample.drop('PRICE', axis=1)  # Features
y = df_sample['PRICE']  # Target variable

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

7. 모델 훈련

이 섹션에서는 학습 데이터를 사용하여 선형 회귀 모델을 생성하고 학습하여 특성과 주택 가격 간의 관계를 학습합니다.

# Creating and training the Linear Regression model
lr = LinearRegression()
lr.fit(X_train, y_train)

8. 모델 평가

테스트 세트를 예측하고 MSE(평균 제곱 오차)와 R 제곱 값을 계산하여 모델 성능을 평가합니다.

# Making predictions on the test set
y_pred = lr.predict(X_test)

# Calculating Mean Squared Error
mse = mean_squared_error(y_test, y_pred)
print(f"\nLinear Regression Mean Squared Error: {mse}")

산출

Linear Regression Mean Squared Error: 0.3699851092128846

9. 실제 값과 예측 값 표시

여기에서는 실제 주택 가격과 모델에서 생성된 예측 가격을 비교하기 위해 DataFrame을 생성합니다.

# Displaying Actual vs Predicted Values
results = pd.DataFrame({'Actual Prices': y_test.values, 'Predicted Prices': y_pred})
print("\nActual vs Predicted:")
print(results)

산출

Actual vs Predicted:
     Actual Prices  Predicted Prices
0          0.87500          0.887202
1          1.19400          2.445412
2          5.00001          6.249122
3          2.78700          2.743305
4          1.99300          2.794774
..             ...               ...
135        1.62100          2.246041
136        3.52500          2.626354
137        1.91700          1.899090
138        2.27900          2.731436
139        1.73400          2.017134

[140 rows x

 2 columns]

10. 결과 시각화

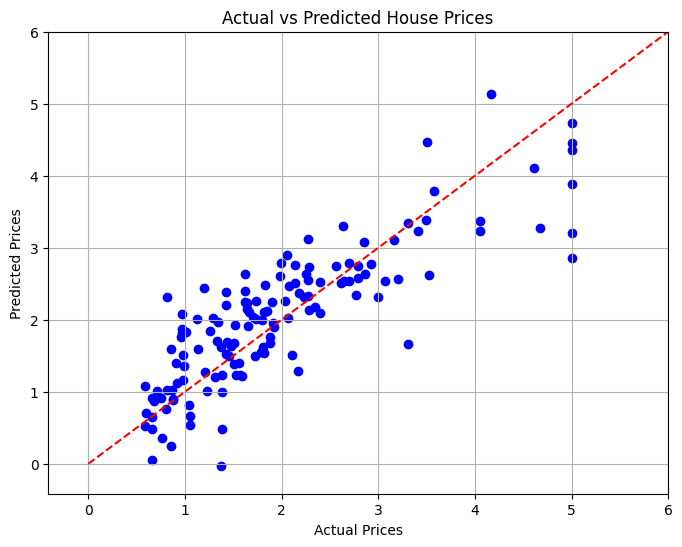
마지막 섹션에서는 모델의 성능을 시각적으로 평가하기 위해 분산형 차트를 사용하여 실제 주택 가격과 예측 주택 가격 간의 관계를 시각화합니다.

# Visualizing the Results
plt.figure(figsize=(8, 6))
plt.scatter(y_test, y_pred, color='blue')
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual vs Predicted House Prices')

# Draw the ideal line
plt.plot([0, 6], [0, 6], color='red', linestyle='--')

# Set limits to minimize empty space
plt.xlim(y_test.min() - 1, y_test.max()   1)
plt.ylim(y_test.min() - 1, y_test.max()   1)

plt.grid()
plt.show()

결론

이 프로젝트에서 우리는 다양한 특성을 기반으로 캘리포니아 주택 가격을 예측하는 선형 회귀 모델을 개발했습니다. 평균 제곱 오차는 모델의 성능을 평가하기 위해 계산되었으며, 이는 예측 정확도의 정량적 측정값을 제공했습니다. 시각화를 통해 모델이 실제 값에 비해 얼마나 잘 수행되는지 확인할 수 있었습니다.

이 프로젝트는 부동산 분석에서 기계 학습의 힘을 보여 주며 더욱 발전된 예측 모델링 기술의 기반이 될 수 있습니다.