카지노가 항상 승리하는 이유가 궁금하신가요? "확률 극복: 카지노 이익 뒤에 숨은 수학"에서는 카지노가 장기적으로 수익을 창출할 수 있도록 하는 간단한 수학과 기발한 전략을 살펴보겠습니다. 이해하기 쉬운 예와 몬테카를로 시뮬레이션을 통해 집 가장자리 뒤에 숨겨진 비밀을 밝혀내겠습니다. 카지노가 어떻게 승률을 유리하게 바꾸는지 알아보세요!

하우스 엣지 이해하기

하우스 에지는 카지노 세계의 기본 개념입니다. 이는 카지노가 플레이어의 각 베팅에서 얻을 것으로 기대하는 평균 이익을 나타냅니다. 본질적으로, 카지노가 장기적으로 유지하게 될 각 베팅의 비율입니다.

카지노에서는 게임의 "실제 확률"에 따라 승리한 베팅을 지급하지 않기 때문에 하우스 에지가 존재합니다. 실제 확률은 사건이 발생할 실제 확률을 나타냅니다. 약간 낮은 확률로 지불함으로써 카지노는 시간이 지남에 따라 이익을 얻도록 보장합니다.

하우스 에지(HE)는 플레이어의 원래 베팅에 대한 백분율로 표시되는 카지노 수익으로 정의됩니다.

** 유럽식 룰렛 **에는 녹색 0이 하나만 있어 총 37개의 숫자가 제공됩니다. 플레이어가 빨간색에 1달러를 걸면 1달러를 얻을 확률은 18/37이고 1달러를 잃을 확률은 19/37입니다. 예상 값은 다음과 같습니다:

기대값=( 1 × 18/37 ​) ( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≒ −2.7%

따라서 유럽식 룰렛에서 하우스 에지(HE)는 약 2.7%입니다.

좀 더 이해하기 쉽게 우리만의 게임, 간단한 주사위 굴리기 게임을 만들어 보겠습니다.

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll 

이 게임에서:

• 롤이 100이면 플레이어의 패배 확률은 1/100입니다.

• 굴림 값이 1에서 50 사이인 경우 플레이어의 패배 확률은 50/100입니다.

• 롤이 51에서 99 사이인 경우 플레이어의 승리 확률은 49/100입니다.

기대값 =(1× 49/100​) ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100 ​ ≒ −2%

따라서 하우스 에지는 2%입니다.

몬테카를로 시뮬레이션 이해

몬테카를로 시뮬레이션은 프로세스에 대한 수많은 시뮬레이션을 실행하고 결과를 관찰함으로써 복잡한 시스템을 이해하고 예측하는 데 사용되는 강력한 도구입니다. 카지노의 맥락에서 몬테카를로 시뮬레이션은 다양한 베팅 시나리오를 모델링하여 하우스 에지가 어떻게 장기적인 수익성을 보장하는지 보여줄 수 있습니다. 몬테카를로 시뮬레이션이 어떻게 작동하고 간단한 카지노 게임에 어떻게 적용할 수 있는지 살펴보겠습니다.

몬테카를로 시뮬레이션이란 무엇입니까?

몬테카를로 시뮬레이션에는 무작위 변수를 생성하여 프로세스를 여러 번 시뮬레이션하고 결과를 분석하는 작업이 포함됩니다. 수천 또는 수백만 번의 반복을 수행함으로써 가능한 결과의 분포를 얻고 다양한 이벤트의 가능성에 대한 통찰력을 얻을 수 있습니다.

주사위 굴리기 게임에 몬테카를로 시뮬레이션 적용

앞서 논의한 주사위 굴리기 게임을 모델링하기 위해 몬테카를로 시뮬레이션을 사용하겠습니다. 이는 시간이 지남에 따라 하우스 에지가 게임 수익성에 어떤 영향을 미치는지 이해하는 데 도움이 됩니다.

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins  = 1
        else:
            losses  = 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

결과 해석

이 시뮬레이션에서는 주사위 굴리기 게임을 10,000,000번 실행하여 승패 비율을 관찰합니다. 앞서 계산한 하우스 에지(2%)를 고려하면 패배율이 승리율보다 약간 높을 것으로 예상됩니다.

시뮬레이션을 실행한 후 다음과 같은 결과가 표시될 수 있습니다.

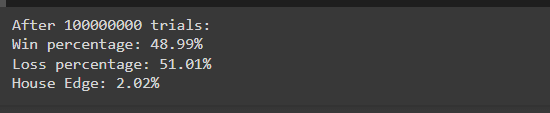
이러한 결과는 이론적 확률(49% 승, 51% 패)과 밀접하게 일치하며, 하우스 에지가 수많은 시행에서 어떻게 나타나는지 보여줍니다. 약간의 불균형은 장기적으로 카지노의 수익성을 보장합니다.

단기 성공과 장기 손실 시각화

몬테카를로 시뮬레이션은 반복되는 무작위 샘플링을 통해 결과를 모델링하고 예측하는 데 강력합니다. 도박의 맥락에서 몬테카를로 시뮬레이션을 사용하여 다양한 베팅 전략의 잠재적 결과를 이해할 수 있습니다.

매 라운드마다 동일한 초기 베팅을 하는 단일 베터를 시뮬레이션하고 지정된 수의 베팅에 걸쳐 계정 가치가 어떻게 변화하는지 관찰합니다.

Matplotlib를 사용하여 베팅 여정을 시뮬레이션하고 시각화하는 방법은 다음과 같습니다.

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager 



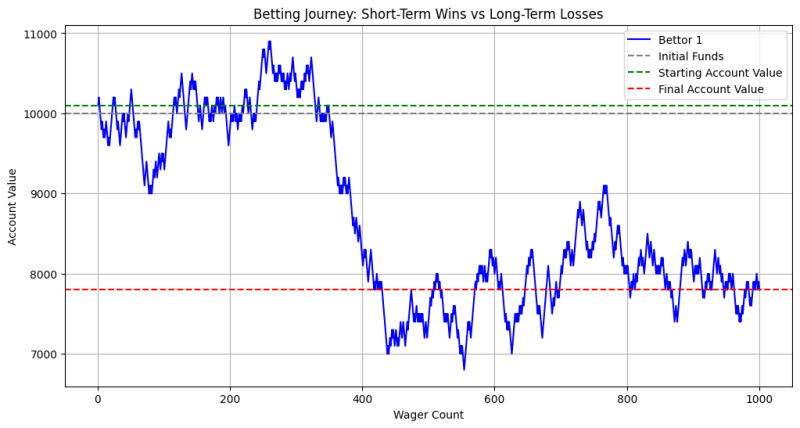
이 그래프는 베터의 계정 가치가 승패로 인해 시간이 지남에 따라 어떻게 변동할 수 있는지 보여줍니다. 처음에는 승리하는 기간(시작 값 위의 녹색 선)이 있을 수 있지만 베팅 횟수가 증가함에 따라 하우스 에지의 누적 효과가 분명해집니다. 결국 베터의 계정 가치는 초기 자금(회색 선) 이하로 하락하는 경향이 있으며 이는 장기적인 손실을 나타냅니다.


  
  
  결론


카지노 수익 이면의 수학을 이해하면 하우스 에지 개념을 통해 모든 게임에서 하우스에 대한 명확한 이점이 드러납니다. 가끔 승리하더라도 카지노 게임에 내재된 확률로 인해 대부분의 플레이어는 시간이 지남에 따라 돈을 잃을 수 있습니다. 몬테 카를로 시뮬레이션은 이러한 역학을 생생하게 보여주며, 카지노의 통계적 이점으로 인해 단기적인 승리가 어떻게 장기적인 손실을 가릴 수 있는지 보여줍니다. 카지노 수익성의 수학적 확실성에 대한 이러한 통찰력은 정보에 입각한 의사 결정과 책임감 있는 도박 관행의 중요성을 강조합니다.

다음으로 다양한 베팅 전략을 비교하거나 다양한 초기 베팅이 베터의 결과에 미치는 영향을 분석하는 등 추가 시각화 또는 변형을 탐색할 수 있습니다.

대기 중:

• GitHub: ezhillragesh

• 트위터: ezhillragesh

• 웹사이트: ragesh.me

주저하지 말고 생각을 공유하고, 질문하고, 토론에 참여하세요.

즐거운 코딩하세요!