もし直線、楕円、円しか使えなかったら、滑らかなラインと複雑な外観を持つ車をデザインするのは難しくないと思いませんか?

1962 年、フランスの技術者ピエール ベジェがベジェ曲線を発表し、最初は自動車の本体設計に使用されました。

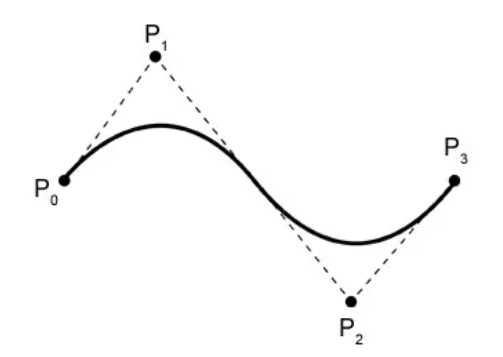
ベジェ曲線は、一連の制御点を通る滑らかな曲線を定義できます。曲線は常に最初と最後の制御点を通過し、中間の制御点の形状の影響を受けます。さらに、ベジェ曲線には凸包の特性があります。

ベジェ曲線は、アニメーション、フォント デザイン、工業デザインなどのコンピュータ グラフィックスや画像モデリングで広く使用されています。

式

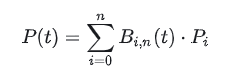
これを理解しましょう。

P(t) は、t における曲線上の点を表します (t は 0 から 1 までの値を持つ分数です)。曲線上の t の点は何ですか?一般的な曲線の説明は、y = f(x) です。ここでは、P(t) を f(x) として理解しましょう。違いは、P(t) がパラメトリック表現 (計算結果は [x, y] のような「ベクトル」) であることです。これについては後で詳しく説明します。

次に、Pi は i 番目の制御点を表します (i は 0 から始まります)。上図を例にとると、P0、P1、P2、P3 の 4 つの制御点があります。式の n は制御点の最後のインデックス、つまり n = 3 (制御点の数ではなく、カウントから 1 を引いた値であることに注意してください)。

Bi,n(t) はバーンスタイン基底関数であり、基底関数としても知られています。特定の (i, n) ごとに、それに対応する異なる基底関数があります。重み付けの観点から理解すると、基底関数は、t の位置の曲線座標に対する i 番目の制御点 Pi の「寄与」を示す重み関数と考えることができます。

基底関数の式は次のとおりです。

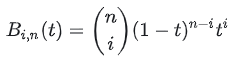
$\left(\genfrac{}{}{0px}{}{n}{i}\right)$( in) 組み合わせの番号です (n から i を選択する方法は何通りありますか?)。基底関数がこのようになる理由については、De Casteljau アルゴリズムと関連付けて理解できます (本文後半を参照)

P(t) の式に戻ります。 ${\sum }_{i=0}^n$∑i=0n は加算記号であり、後続の部分 ( $B_{i、n}(t)\cdot P_i$Bi,n(t )⋅Pi ) は i=0 から i=n まで合計されます。

上の図を例として、P(0.1)を計算したいと仮定すると、どのように計算すればよいでしょうか?次のように展開されます:

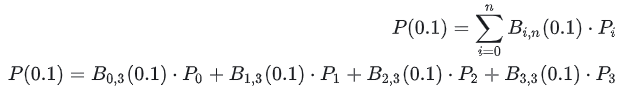
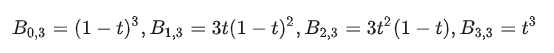
t=0.1 を代入して次を取得します:

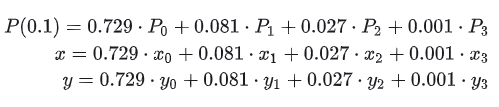
曲線のパラメトリック表現

ここではネチズンからの記事を直接引用します (リンク)

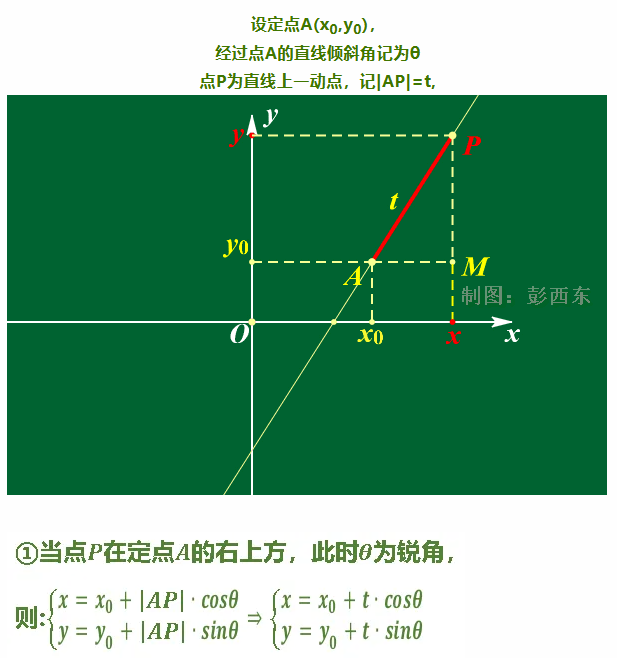
上の式に注目してみましょう。

上の図に示すように、私たちがよく知っている直線は別の観点から理解できます。t (つまり、点 P から既知の点 (x0,y0) までの |AP| の長さ) を使用すると、この場合、点 P は上記の三角関数によって決定できます。

より一般的には、次のように記述できます:

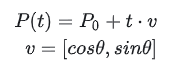
ここで、P0 はベクトル [x0,y0] であり、v もベクトルです。足し合わせると、P(t) はベクトル [x,y].

もう一度円を見てみる:

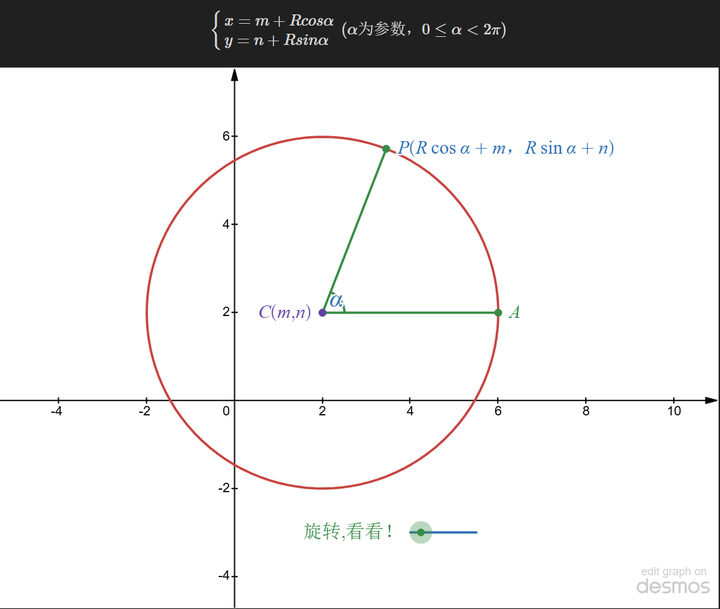
図に示すように、円は既知の中心を持ち、円上の任意の点は回転角度と半径によって決定されるとみなすことができます。次のように書くこともできます:

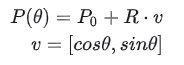
パラメトリック方程式は幾何学的不変性を維持し、円のような形状を表現できます (1 つの x が複数の y 値に対応します)。

デ・カステルジョ

De Casteljau アルゴリズムは、描画やその他の操作のためにベジェ曲線を評価および近似するために実際のアプリケーションで使用される方法です。以前の定義ベースの評価方法と比較して、より高速かつ安定しており、ベジェ曲線の特性に近くなります。

ここでは、link1 と link2 の 2 つの記事を参照します

まず、次のように定義します。

上のβを見てください。上付き文字と下付き文字が少しわかりにくいです。次の三角再帰を理解するために使用できます:

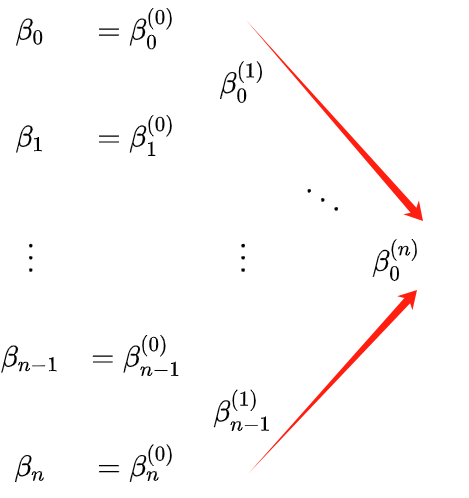
上図の三角形の赤い端は、t0 で割られた 2 つのセグメントの制御点です。 t0、P(t0) をより明確に理解するには、 ${\beta }_0^{(n)}$β0(n) ）、2 つの曲線の制御点については、次の図を参照してください:

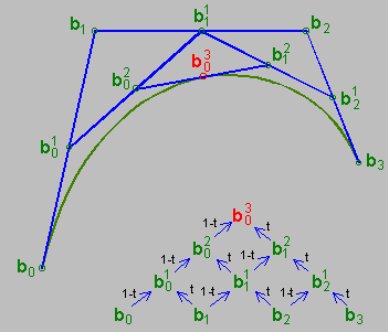
上の図は、t=0.5 の場合のさまざまな点間の関係を示しています。

「補間」の観点から見ると、計算プロセスは次のようにも理解できます。

1. 隣接する制御点の各ペアの中点 (t=0.5 のため)、つまり b01、b11、b21 を求めます (表記はご容赦ください。LaTeX で書くのは面倒です)
2. b01−b11 上で中点 b02 を見つけ、b11-b21 上で中点 b12 を見つけます
3. b02−b12 の中点 b03 を見つける ​ 実際、De Casteljau アルゴリズムの本質は補間と反復です。

ド・カステルジョーに基づく曲線描画

現在、2 つの方法が確認されています。

1 つの方法では、小さなステップ増分で 0 から 1 まで t を移動します（つまり、 0.01）。 P(t) が求められるたびに、再帰式を使用して決定されます。 ${\beta }_0^{(n)}$β0(n) .

もう 1 つの方法では、P(t=0.5) を求め、次に分割された 2 つの曲線について、それぞれ P(t=0.5) を求めます。この細分化は、曲線が近似されるまで続きます。

実装

練習せずにただ見ているだけというのは、いつも非現実的な気分になります。

そこで、曲線描画用の独自の実装コードを作成し、それをツールキットに編成しました: Compilelife のツールキット

対応するコアコードはこちら