はじめに 1

関数がそれ自体を呼び出すプロセスは再帰と呼ばれ、
対応する関数は 再帰関数.
と呼ばれます。 コンピュータープログラミングは数学の基本的な応用なので、let
まず、再帰の背後にある数学的推論を理解しようとします。
一般に、関数の概念は誰もが知っています。簡単に言うと、関数は
です。 入力を与えると出力を生成する数式。例えば：
関数 F(x) が次のように定義される関数であるとします。 F(x) = x^2 4
この関数の Java コードは次のように記述できます:

パブリック 静的 int F(int x){
return (x * x 4);
}

これで、x のさまざまな値をこの関数に渡して、出力を受け取ることができます
それに応じて。
再帰に進む前に、別の数学的
を理解してみましょう。 数学的帰納法 (PMI) の原理.

数学的帰納法 (PMI) は、ステートメントを証明するためのテクニックです。
式、または自然数の集合について主張される定理。
があります 次の 3 つの手順:
1.** 自明なケースのステップ*: このステップでは、
に対する目的のステートメントを証明します。 n = 0 または n = 1 のような基本ケース。
2.* 仮定のステップ**: このステップでは、目的のステートメント
を仮定します。 n = k.

1. ステップを証明するには: 仮定ステップの結果から、次のことを証明します。 n = k が true である場合は常に、目的の方程式に対して n = k 1 も true になります。

例: 数学的帰納法原理を使用して次のことを証明してみましょう:
S(N): 1 2 3 ... N = (N * (N 1))/2
(最初の N 個の自然数の合計)
証拠：
ステップ 1: N = 1 の場合、S(1) = 1 は真です。
ステップ 2: 指定されたステートメントが N = k に対して true、つまり
であると仮定します。 1 2 3 .... k = (k * (k 1))/2
ステップ 3: ステップ 2 を使用して、N = k 1 のステートメントを証明しましょう。

証明するには: 1 2 3 ... (k 1) = ((k 1)*(k 2))/2
証拠：

ステップ 2 で得られた結果の LHS と RHS の両方に (k 1) を追加します:
1 2 3 ... (k 1) = (k*(k 1))/2 (k 1)

さて、RHS 側から共通の (k 1) を取り出します:
1 2 3 ... (k 1) = (k 1)*((k 2)/2)

私たちが証明しようとしている声明によると:
1 2 3 ... (k 1) = ((k 1)*(k 2))/2
したがって証明されました。

再帰の働き

上記の 3 つを要約することで、再帰的アプローチのステップを定義できます
ステップ:
● 基本ケース: 再帰関数には、
という終了条件が必要です。 プロセスはそれ自体の呼び出しを停止します。このようなケースは基本ケースとして知られています。基本ケースがないと、自分自身を呼び出し続け、
でスタックしてしまいます。 無限ループ。すぐに、再帰の深さ*を超えて、
がスローされます。 エラー。
● 再帰呼び出し: 再帰関数は、より小さいバージョンでそれ自体を呼び出します
主な問題の。このステップをそのまま書くときは注意が必要です
小さな問題が何なのかを正しく理解することが重要です。
● 小規模な計算: 通常、再帰的
ごとに計算ステップを実行します。 電話。この計算ステップは、再帰呼び出し
の前後に実行できます。 問題の性質によって異なります。

注: 再帰では、再帰呼び出しを保存する組み込みスタックが使用されます。したがって、
メモリのオーバーフローを避けるために、再帰呼び出しの数はできるだけ少なくする必要があります。もし
再帰呼び出しの数が最大許容量を超えています、
**再帰の深さ** を超えます。
ここで、Recursion

問題ステートメント - 数値の階乗を求める

アプローチ: PMI の 3 つのステップを理解し、
を使用して同じものを関連付けます。 再帰

1. 帰納法ステップ: 数値 n - F(n) の階乗の計算 帰納仮説: n-1 - F(n-1)
の階乗はすでに得られています。
2. F(n) を F(n-1) で表現すると、F(n)=n*F(n-1) になります。したがって、
が得られます。

public static int fat(int n){
int ans = ファクト(n-1); #仮定ステップ
ans * n を返します。 #仮定のステップから問題を解く
}

1. コードはまだ完成していません。欠品しているのはベースケースです。さあ、そうします 予行演習を行って、再帰を停止する必要があるケースを見つけます。 n = 5:
を考えてみましょう。

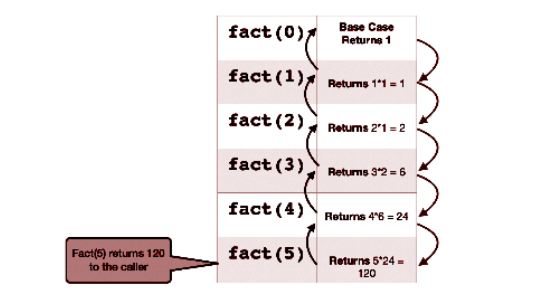
上でわかるように、n = 0、つまり 1 の答えはすでにわかっています。 これを基本ケースとして保持してください。したがって、コードは次のようになります:

if (n == 0) // 基本ケース
1 を返す;
それ以外
n*factorial(n-1) を返します。 // 再帰的なケース
}