これまでさまざまな並べ替えアルゴリズムについて説明してきましたが、今日は選択並べ替えアルゴリズムについて学びます。メモリに制約のある環境で可能な最小限のスワップを可能にする並べ替えアルゴリズム。

目次

1. 導入
2. 選択ソートアルゴリズムとは何ですか?
3. 選択の並べ替えはどのように機能しますか?
   • 時間計算量
   • 空間の複雑さ
4. JavaScript での実装
5. LeetCode の問題の解決
6. 結論

導入

選択ソートは、リストの未ソート部分から最小 (または最大) 要素を繰り返し選択し、それをソート済み部分の先頭 (または末尾) に移動する、シンプルかつ効果的なソート アルゴリズムです。このプロセスは、リスト全体がソートされるまで繰り返されます。この記事では、選択ソート アルゴリズム、JavaScript でのその実装、および現実世界の問題解決におけるそのアプリケーションの詳細を詳しく説明します。

選択ソートアルゴリズムとは何ですか?

選択ソート アルゴリズムは、インプレース比較ソート アルゴリズムです。入力リストを 2 つの部分に分割します:

1. 左端のソート部分
2. 右端の未ソート部分

アルゴリズムは、未ソート部分から最小の要素を繰り返し選択し、それを左端の未ソート要素と交換し、ソート済み部分と未ソート部分の境界を 1 要素右に移動します。

選択の並べ替えはどのように機能しますか?

配列 [64, 25, 12, 22, 11]:

1. 初期配列: [64, 25, 12, 22, 11]

• ソート部分: []
• 未ソート部分: [64, 25, 12, 22, 11]

1. 最初のパス:

• 未ソート部分の最小値を検索: 11
• 11 をソートされていない最初の要素 (64) と交換します
• 結果: [11, 25, 12, 22, 64]
• ソート部分: [11]
• 未ソート部分: [25, 12, 22, 64]

1. 2 番目のパス:

• 未ソート部分の最小値を検索: 12
• 12 をソートされていない最初の要素 (25) と交換します
• 結果: [11, 12, 25, 22, 64]
• ソートされた部分: [11, 12]
• 未ソート部分: [25, 22, 64]

1. 3 番目のパス:

• 未ソート部分の最小値を検索: 22
• 22 をソートされていない最初の要素 (25) と交換します
• 結果: [11, 12, 22, 25, 64]
• ソートされた部分: [11, 12, 22]
• 未ソート部分: [25, 64]

1. 4 番目のパス:

• 未ソート部分の最小値を検索: 25
• 25 はすでに正しい位置にあります
• 結果: [11, 12, 22, 25, 64]
• ソートされた部分: [11, 12, 22, 25]
• 未ソート部分: [64]

1. 最終パス:
   • 残りの要素は 1 つだけです。自動的に正しい位置に配置されます
   • 最終結果: [11, 12, 22, 25, 64]

配列は完全にソートされました。

時間計算量

選択ソートの時間計算量は、すべてのケース (最良、平均、最悪) で O(n^2) です。ここで、n は配列内の要素の数です。その理由:

• 外側のループは n-1 回実行されます
• 外側のループの反復ごとに、内側のループが n-i-1 回実行されます (i は外側のループの現在の反復です)

これにより、約 (n^2)/2 の比較と n 回のスワップが行われ、O(n^2) に単純化されます。

この二次時間計算量のため、選択並べ替えは大規模なデータセットに対して効率的ではありません。ただし、そのシンプルさとスワップの回数を可能な限り最小限に抑えるという事実により、特定の状況、特に補助メモリが限られている場合には便利です。

空間の複雑さ

Selection Sort は配列をその場でソートするため、空間複雑度は O(1) です。入力サイズに関係なく、一定量の追加メモリ空間のみが必要です。これによりメモリ効率が向上し、メモリに制約のある環境では有利になります。

JavaScriptでの実装

これは、選択並べ替えアルゴリズムの JavaScript 実装です:

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


コードを分解してみましょう:

配列を入力として受け取る関数selectionSortを定義します。
外側のループ (i) で配列を繰り返し処理します。これは、並べ替えられた部分と並べ替えられていない部分の境界を表します。
反復ごとに、ソートされていない最初の要素が最小であると想定し、そのインデックスを保存します。
次に、内部ループ (j) を使用して、ソートされていない部分の実際の最小要素を見つけます。
より小さい要素が見つかった場合は、minIndex を更新します。
最小値を見つけた後、必要に応じて、それをソートされていない最初の要素と交換します。
配列全体がソートされるまでこのプロセスを繰り返します。

  
  
  LeetCode の問題の解決


選択ソート アルゴリズムを使用して、leetcode アルゴリズムの問​​題を 1 つ解いてみましょう。しましょうか？

  
  
  問題: 配列のソート [中]


問題: 整数 num の配列を指定して、配列を昇順に並べ替えて返します。組み込み関数を使用せずに、O(nlog(n)) の時間計算量と可能な限り最小の空間計算量で問題を解決する必要があります。

アプローチ:: この問題を解決するには、選択ソート アルゴリズムを直接適用できます。これには、配列を反復処理し、未ソート部分で最小の要素を見つけて、それを最初の未ソート要素と交換することが含まれます。配列全体がソートされるまで、このプロセスを繰り返します。

解決：

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


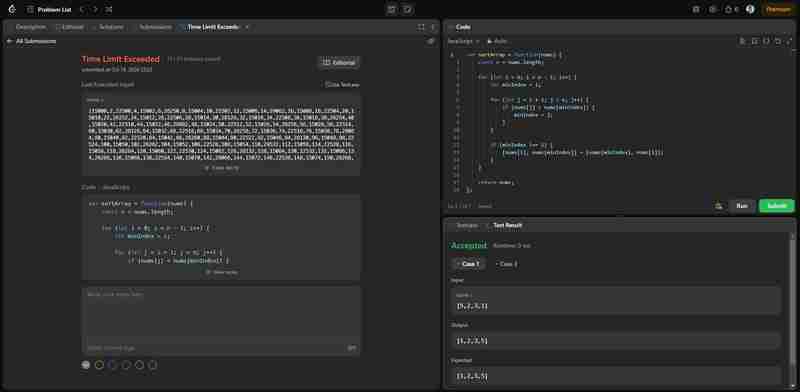
このソリューションは、以前に実装した選択並べ替えアルゴリズムを直接適用します。この問題は正しく解決されますが、選択並べ替えの時間の複雑さは O(n^2) であるため、この解決策は LeetCode での大規模な入力の制限時間を超える可能性があることに注意してください。下の画像は、解決策は正しいものの、効率的ではないことを示しています。



  
  
  結論


 結論として、Selection Sort は、並べ替え技術の世界への優れた入門として機能する、シンプルで直感的な並べ替えアルゴリズムです。そのシンプルさにより、理解と実装が容易となり、初心者にとって価値のある学習ツールとなっています。ただし、二次時間計算量が O(n^2) であるため、大規模なデータセットに対しては効率的ではありません。大規模なデータセットやパフォーマンスが重要なアプリケーションの場合は、QuickSort、MergeSort、または組み込みの並べ替え関数などのより効率的なアルゴリズムが推奨されます。


  
  
  常に最新情報を入手してつながりを保つ


このシリーズのどの部分も見逃さないようにし、さらに詳しく知りたい場合は私と連絡を取ってください

ソフトウェア開発 (Web、サーバー、モバイル、またはスクレイピング / オートメーション)、データに関するディスカッション

構造やアルゴリズム、その他のエキサイティングな技術トピックについては、こちらをフォローしてください:



    
      

        
    
  

    

素晴らしい解決策 ?フォロー

    

      ソフトウェアエンジニア |テクニカルライター |バックエンド、Web およびモバイル開発者 ? |効率的でスケーラブルなソフトウェア ソリューションの作成に情熱を注いでいます。 #接続しましょう ?
    
  

• GitHub
• リンク済み
• X (Twitter)

引き続きコーディングをお楽しみください ?‍??