現実世界の問題の多くは、グラフ アルゴリズムを使用して解決できます。グラフは、現実世界の問題をモデル化して解決するのに役立ちます。たとえば、2 つの都市間の最小フライト数を見つける問題は、次の図に示すように、頂点が都市を表し、エッジが隣接する 2 つの都市間のフライトを表すグラフを使用してモデル化できます。最小乗り継ぎ便数を求める問題
2 つの都市間の計算は、グラフ内の 2 つの頂点間の最短経路を見つけることに帰着します。

グラフ問題の研究は、グラフ理論として知られています。グラフ理論は、1736 年にレオンハルト オイラーによって創設され、有名な ケーニヒスベルクの 7 つの橋 問題を解決するためにグラフ用語を導入しました。プロイセン州ケーニヒスベルク市（現在のロシアのカリーニングラード）は、プレーゲル川によって分断されました。川には二つの島がありました。下図(a)に示すように、都市と島々は7つの橋で結ばれていました。問題は、散歩をして、各橋を一度だけ渡って、出発点に戻ることができるかということです。オイラーはそれが不可能であることを証明しました。

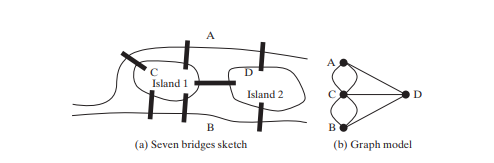
証明を確立するために、オイラーはまずケーニヒスベルクの都市地図をすべての通りを削除して抽象化し、上の図 (a) に示すスケッチを作成しました。次に、図に示すように、各陸地を 頂点 または ノード と呼ばれる点に置き換え、各橋を エッジ と呼ばれる線に置き換えました。上図(b)。頂点とエッジを含むこの構造は、グラフ.

グラフを見て、任意の頂点から始まり、すべてのエッジを 1 回だけ通過し、開始頂点に戻るパスがあるかどうかを調べます。オイラーは、このようなパスが存在するには、各頂点に偶数のエッジが必要であることを証明しました。したがって、ケーニヒスベルクの七つの橋問題には解決策がありません。

グラフの問題は、アルゴリズムを使用して解決されることがよくあります。グラフ アルゴリズムは、コンピューター サイエンス、数学、生物学、工学、経済学、遺伝学、社会科学など、さまざまな分野で多くの用途があります。

グラフの基本用語

グラフは頂点と、頂点を接続するエッジで構成されます。この章は、グラフ理論や離散数学についての予備知識があることを前提としていません。グラフを定義するために、単純かつ単純な用語を使用します。

グラフとは何ですか?グラフは、現実世界のエンティティ間の関係を表す数学的構造です。たとえば、上図のグラフは都市間の航空便を表し、下図 (b) のグラフは陸地間の橋を表します。

グラフは、空ではない頂点のセット (ノードまたはポイントとも呼ばれます) と、頂点を接続するエッジのセットで構成されます。便宜上、グラフを G = (V, E) として定義します。ここで、V は頂点のセットを表し、E はエッジのセットを表します。たとえば、下図のグラフの V と E は次のようになります。

V = {"シアトル"、"サンフランシスコ"、"ロサンゼルス"、
「デンバー」、「カンザスシティ」、「シカゴ」、「ボストン」、「ニューヨーク」、
"アトランタ"、"マイアミ"、"ダラス"、"ヒューストン"};

E = {{"シアトル", "サンフランシスコ"},{"シアトル", "シカゴ"},
{"シアトル"、"デンバー"}、{"サンフランシスコ"、"デンバー"}、
...
};

グラフは有向または無向の場合があります。 有向グラフでは、各エッジに方向があり、エッジを通ってある頂点から別の頂点に移動できることを示します。有向グラフを使用して親子関係をモデル化できます。頂点 A から B までのエッジは、A が B の親であることを示します。下の図 (a) は有向グラフを示しています。

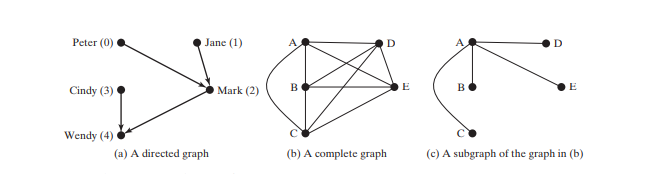
無向グラフでは、頂点間を両方向に移動できます。以下の図のグラフは無向です。

エッジは重み付けすることも、重み付けしないこともできます。たとえば、上の図のグラフの各エッジに重みを割り当てて、2 つの都市間の飛行時間を示すことができます。

2 つの頂点が同じエッジで接続されている場合、それらの頂点は 隣接している と言われます。同様に、2 つのエッジが同じ頂点に接続されている場合、それらのエッジは 隣接している と言われます。 2 つの頂点を結ぶグラフ内のエッジは、両方の頂点に対して入射していると言われます。頂点の 次数 は、それに付随するエッジの数です。

2 つの頂点が隣接している場合、その頂点は 隣接と呼ばれます。同様に、2 つのエッジが隣接している場合は、隣接と呼ばれます。

ループは、頂点をそれ自体にリンクするエッジです。 2 つの頂点が 2 つ以上のエッジで接続されている場合、これらのエッジは 平行エッジ と呼ばれます。 単純なグラフは、ループや平行エッジを持たないグラフです。 完全なグラフでは、下の図 (b) に示すように、頂点の 2 つのペアごとに接続されます。

接続されています。グラフ G の サブグラフ は、頂点セットが G のサブセットであり、エッジ セットが G のサブセットであるグラフです。たとえば、上の図 (c) のグラフは、上図 (b) のグラフのサブグラフ。

サイクルは、頂点から始まり同じ頂点で終わる閉じたパスです。接続されたグラフは、サイクルを持たない場合、ツリーになります。グラフ G の スパニング ツリー は G の接続されたサブグラフであり、そのサブグラフは G のすべての頂点を含むツリーです。