このセクションでは、繰り返し、シーケンス、選択ステートメントの Big O を決定する例をいくつか示します。

例1

次のループの時間計算量を考えてみましょう:

for (int i = 1; i k = k 5;
}

実行するための一定時間 c です

k = k 5;

ループは n 回実行されるため、ループの時間計算量は

T(n) = (定数 c)*n = O(n).

理論分析により、アルゴリズムのパフォーマンスが予測されます。このアルゴリズムがどのように実行されるかを確認するには、以下のプログラムのコードを実行して、n = 1000000、10000000、100000000、および 100000000 の実行時間を取得します。

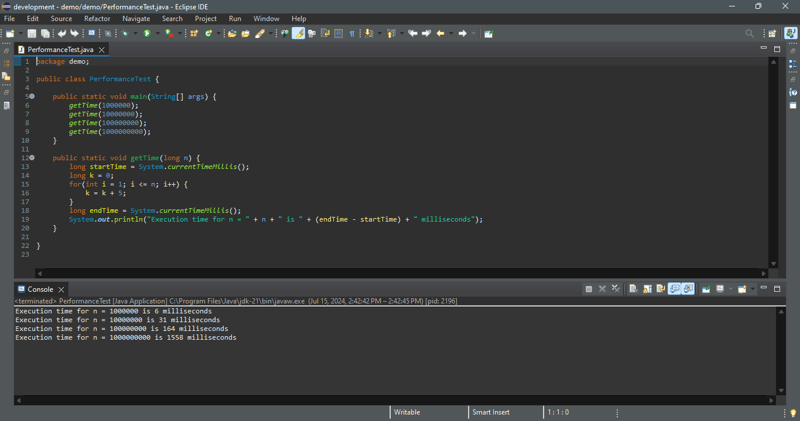
私たちの分析では、このループの線形時間計算量が予測されます。サンプル出力に示されているように、入力サイズが 10 倍に増加すると、実行時間は約 10 倍に増加します。実行は予測を裏付けます。

例 2

次のループの時間計算量はどれくらいですか?

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

実行するための一定時間 c です

k = k i j;

外側のループは n 回実行されます。外側のループの反復ごとに、内側のループが n 回実行されます。したがって、ループの時間計算量は

T(n) = (定数 c)*n*n = O(n^2)

時間計算量が O(n^2) のアルゴリズムは、二次アルゴリズムと呼ばれ、二次成長率を示します。二次アルゴリズムは、問題のサイズが大きくなるにつれて急速に大きくなります。入力サイズを 2 倍にすると、アルゴリズムの時間は 4 倍になります。ネストされたループを含むアルゴリズムは、多くの場合 2 次です。

例 3

次のループを考えてみましょう:

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

外側のループは n 回実行されます。 i = 1, 2, c の場合、内側のループは 1 回、2 回、および n 回実行されます。したがって、ループの時間計算量は

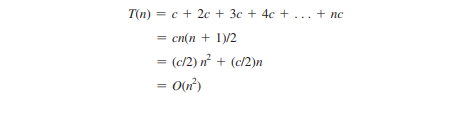
例 4

次のループを考えてみましょう:

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

内側のループは 20 回実行され、外側のループは n 回実行されます。したがって、ループの時間計算量は

T(n) = 20*c*n = O(n)

例5

次のシーケンスを考えてみましょう:

for (int j = 1; j k = k 4;
}

for (int i = 1; i for (int j = 1; j k = k i j;
}
}

最初のループは 10 回実行され、2 番目のループは 20 * n 回実行されます。したがって、ループの時間計算量は

T(n) = 10*c 20*c*n = O(n)

例6

次の選択ステートメントを考えてみましょう:

if (list.contains(e)) {
System.out.println(e);
}
それ以外
for (オブジェクト t: リスト) {
System.out.println(t);
}

リストに n 個の要素が含まれているとします。 list.contains(e) の実行時間は O(n) です。 else 句のループには O(n) 時間がかかります。したがって、ステートメント全体の時間計算量は

例 7

整数 n に対する a^n の計算を考えてみましょう。単純なアルゴリズムでは、次のように a を n 回乗算します:

結果 = 1;
for (int i = 1; i 結果 *= a;

アルゴリズムには O(n) 時間がかかります。一般性を失わずに、n = 2^k と仮定します。次のスキームを使用してアルゴリズムを改善できます:

結果 = a;
for (int i = 1; i 結果 = 結果 * 結果;

アルゴリズムには O(logn) 時間がかかります。任意の n について、アルゴリズムを修正して、複雑さが依然として O(logn) であることを証明できます。

簡単にするために、0(logn) = 0(log2n) = 0(logan) であるため、定数の基数は省略されます。