भारित नौ पूंछ समस्या को भारित सबसे छोटे पथ की समस्या में कम किया जा सकता है।
अनुभाग ने नौ पूंछ समस्या प्रस्तुत की और बीएफएस एल्गोरिथ्म का उपयोग करके इसे हल किया। यह अनुभाग समस्या की विविधता प्रस्तुत करता है और इसे सबसे छोटे-पथ एल्गोरिदम का उपयोग करके हल करता है।

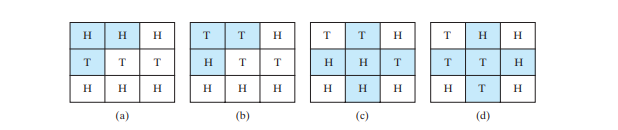
नौ पूंछ वाली समस्या उन चालों की न्यूनतम संख्या ज्ञात करना है जो सभी सिक्कों को नीचे की ओर ले जाती हैं। प्रत्येक चाल एक प्रमुख सिक्का और उसके पड़ोसियों को उछालती है। भारित नौ पूंछ समस्या प्रत्येक चाल पर भार के रूप में फ़्लिप की संख्या निर्दिष्ट करती है। उदाहरण के लिए, आप पहली पंक्ति के पहले सिक्के और उसके दो पड़ोसियों को उछालकर चित्र के नीचे दिए गए सिक्कों को चित्र के नीचे दिए गए बी के सिक्कों में बदल सकते हैं। इस प्रकार, इस चाल का भार 3 है। आप बीच वाले सिक्के और उसके चार पड़ोसियों को उछालकर नीचे चित्र c में सिक्कों को चित्र नीचे d में बदल सकते हैं। तो इस कदम का भार 5 है।

भारित नौ पूंछ समस्या को किनारे-भारित ग्राफ़ में शुरुआती नोड से लक्ष्य नोड तक सबसे छोटा रास्ता खोजने के लिए कम किया जा सकता है। ग्राफ़ में 512 नोड हैं। यदि नोड u से नोड v की ओर कोई कदम है, तो नोड v से u तक बढ़त बनाएं। किनारे के वजन के रूप में फ्लिप की संख्या निर्धारित करें।

याद रखें कि अनुभाग में हमने नौ पूंछ समस्या के मॉडलिंग के लिए एक वर्ग NineTtailModel को परिभाषित किया था। अब हम WeightedNineTtailModel नामक एक नई कक्षा को परिभाषित करते हैं जो NineTAILModel का विस्तार करती है, जैसा कि नीचे चित्र में दिखाया गया है।

NineTtailModel वर्ग एक ग्राफ़ बनाता है और लक्ष्य नोड 511 पर निहित एक ट्री प्राप्त करता है। वेटेडनाइनटेलमॉडल, नाइनटेलमॉडल के समान है, सिवाय इसके कि यह एक वेटेडग्राफ बनाता है और लक्ष्य नोड पर निहित एक ShortestPathTree प्राप्त करता है 511। वेटेडनाइनटेलमॉडल का विस्तार नाइनटेलमॉडल है। विधि getEdges() ग्राफ़ में सभी किनारों को ढूंढती है। getNumberOfFlips(int u, int v) विधि नोड u से नोड v तक फ़्लिप की संख्या लौटाती है। getNumberOfFlips(int u) विधि नोड u से लक्ष्य नोड तक फ़्लिप की संख्या लौटाती है।

नीचे दिया गया कोड WeightedNineTtailModel को लागू करता है।

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}

WeightedNineTtailModel भारित नौ पूंछ समस्या (पंक्तियाँ 10-11) को मॉडल करने के लिए एक WeightedGraph बनाने के लिए NineTtailModel का विस्तार करता है। प्रत्येक नोड के लिए u, getEdges() विधि एक फ़्लिप नोड ढूंढती है v और किनारे के लिए वजन के रूप में फ़्लिप की संख्या निर्दिष्ट करती है (v, u) (पंक्ति 30)। getNumberOfFlips(int u, int v) विधि नोड u से नोड v (पंक्तियाँ 38-47) तक फ़्लिप की संख्या लौटाती है। फ़्लिप की संख्या
के बीच विभिन्न कोशिकाओं की संख्या है दो नोड्स (पंक्ति 44).

WeightedNineTtailModel लक्ष्य नोड 511 (पंक्ति 14) पर निहित एक ShortestPathTree प्राप्त करता है। ध्यान दें कि tree एक संरक्षित डेटा फ़ील्ड है जो NineTtailModel में परिभाषित है और ShortestPathTree Tree का एक उपवर्ग है। NineTtailModel में परिभाषित विधियां tree संपत्ति का उपयोग करती हैं।

getNumberOfFlips(int u) विधि (पंक्तियाँ 49-52) नोड u से लक्ष्य नोड तक फ़्लिप की संख्या लौटाती है, जो नोड से पथ की लागत है u लक्ष्य नोड पर। यह लागत ShortestPathTree वर्ग (पंक्ति 51) में परिभाषित getCost(u) विधि को लागू करके प्राप्त की जा सकती है।

नीचे दिया गया कोड एक प्रोग्राम देता है जो उपयोगकर्ता को प्रारंभिक नोड दर्ज करने के लिए प्रेरित करता है और लक्ष्य नोड तक पहुंचने के लिए फ़्लिप की न्यूनतम संख्या प्रदर्शित करता है।

package demo;

import java.util.Scanner;

public class WeightedNineTail {

    public static void main(String[] args) {
        // Prompt the user to enter nine coins' Hs and Ts
        System.out.print("Enter the initial nine coins Hs and Ts: ");
        Scanner input = new Scanner(System.in);
        String s = input.nextLine();
        char[] initialNode = s.toCharArray();

        WeightedNineTailModel model = new WeightedNineTailModel();
        java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode));

        System.out.println("The steps to flip the coins are ");
        for (int i = 0; i 



शुरुआती नौ सिक्के Hs और Ts दर्ज करें: HHHTTTHHH

सिक्के उछालने के चरण हैं

HHH

टीटीटी

HHH

HHH

टीएचटी

टीटीटी

टीटीटी

टीटीटी

टीटीटी

फ़्लिप की संख्या 8 है

प्रोग्राम उपयोगकर्ता को पंक्ति 8 में एक स्ट्रिंग के रूप में Hs और Ts के संयोजन के साथ नौ अक्षरों के साथ एक प्रारंभिक नोड दर्ज करने के लिए प्रेरित करता है, वर्णों की एक सरणी प्राप्त करता है स्ट्रिंग (पंक्ति 9), एक मॉडल (पंक्ति 11) बनाती है, प्रारंभिक नोड से लक्ष्य नोड (पंक्तियाँ 12-13) तक सबसे छोटा पथ प्राप्त करती है, पथ में नोड्स प्रदर्शित करती है (पंक्तियाँ 16-17), और लक्ष्य नोड (पंक्ति 20) तक पहुंचने के लिए आवश्यक फ़्लिप की संख्या प्राप्त करने के लिए getNumberOfFlips को आमंत्रित करता है।