कल्पना करें यदि आप केवल सीधी रेखाओं, दीर्घवृत्त और वृत्तों का उपयोग कर सकते हैं, तो क्या चिकनी रेखाओं और जटिल उपस्थिति वाली कार को डिजाइन करना मुश्किल नहीं होगा?

1962 में, फ्रांसीसी इंजीनियर पियरे बेज़ियर ने बेज़ियर कर्व प्रकाशित किया, जिसका उपयोग शुरू में कारों के मुख्य बॉडी डिज़ाइन के लिए किया गया था।

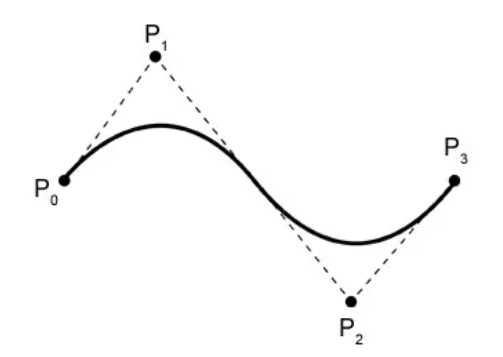
बेज़ियर वक्र नियंत्रण बिंदुओं की एक श्रृंखला के माध्यम से एक चिकनी वक्र को परिभाषित कर सकते हैं। वक्र हमेशा पहले और आखिरी नियंत्रण बिंदुओं से होकर गुजरता है और मध्यवर्ती नियंत्रण बिंदुओं के आकार से प्रभावित होता है। इसके अतिरिक्त, बेज़ियर वक्रों में उत्तल पतवारों का गुण होता है।

बेज़ियर कर्व्स का व्यापक रूप से कंप्यूटर ग्राफिक्स और छवि मॉडलिंग में उपयोग किया जाता है, जैसे एनीमेशन, फ़ॉन्ट डिज़ाइन और औद्योगिक डिज़ाइन में।

FORMULA

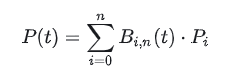
आइये इसे समझते हैं।

पी(टी) टी पर वक्र पर एक बिंदु का प्रतिनिधित्व करता है (टी एक अंश है, जिसका मान 0 से 1 तक है)। वक्र पर t पर एक बिंदु क्या है? एक सामान्य वक्र विवरण है: y = f(x), और अभी के लिए, आइए P(t) को f(x) के रूप में समझें। अंतर यह है कि P(t) एक पैरामीट्रिक प्रतिनिधित्व है (और गणना परिणाम एक "वेक्टर" है जैसे [x, y]), जिसे बाद में विस्तार से समझाया जाएगा।

इसके बाद, पाई आई-वें नियंत्रण बिंदु का प्रतिनिधित्व करता है (आई 0 से शुरू होता है)। उपरोक्त चित्र को उदाहरण के रूप में लेते हुए, 4 नियंत्रण बिंदु हैं, जो P0, P1, P2, P3 हैं। सूत्र में n नियंत्रण बिंदुओं का अंतिम सूचकांक है, यानी, n = 3 (ध्यान दें कि यह नियंत्रण बिंदुओं की संख्या नहीं है, बल्कि गिनती शून्य से 1 है)।

Bi,n(t) बर्नस्टीन आधार फ़ंक्शन है, जिसे आधार फ़ंक्शन के रूप में भी जाना जाता है। प्रत्येक विशिष्ट (i, n) के लिए, उसके अनुरूप एक अलग आधार फ़ंक्शन होता है। यदि आप भारित परिप्रेक्ष्य से समझते हैं, तो आप आधार फ़ंक्शन को वज़न फ़ंक्शन के रूप में मान सकते हैं, जो टी की स्थिति में वक्र निर्देशांक में आई-वें नियंत्रण बिंदु पीआई के "योगदान" को दर्शाता है।

आधार फ़ंक्शन का सूत्र इस प्रकार है:

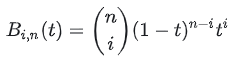
$\left(\genfrac{}{}{0px}{}{n}{i}\right)$( in​) संयोजन संख्या है (n में से i को चुनने के कितने तरीके हैं?)। आधार फ़ंक्शन इस तरह क्यों दिखता है, इसे डी कैस्टेलजौ एल्गोरिदम के संबंध में समझा जा सकता है (पाठ में बाद में देखें)

P(t) सूत्र पर वापस, ${\sum }_{i=0}^n$∑i=0n ​ योग चिह्न है, जो दर्शाता है कि अगला भाग ( $B_{i,n}(t)\cdot P_i$Bi,n​(टी )⋅Pi​ ) का योग i=0 से i=n तक किया जाना है।

उपरोक्त चित्र को एक उदाहरण के रूप में लेते हुए, मान लें कि हम P(0.1) की गणना करना चाहते हैं, इसे कैसे करें? इसका विस्तार इस प्रकार किया गया है:

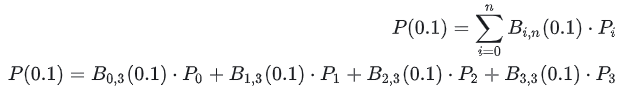
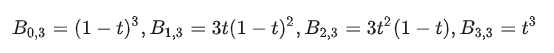
प्राप्त करने के लिए t=0.1 प्रतिस्थापित करें:

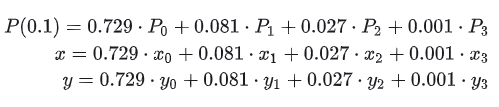
वक्र का पैरामीट्रिक प्रतिनिधित्व

यहां सीधे तौर पर एक नेटिज़न का लेख उद्धृत किया गया है (लिंक)

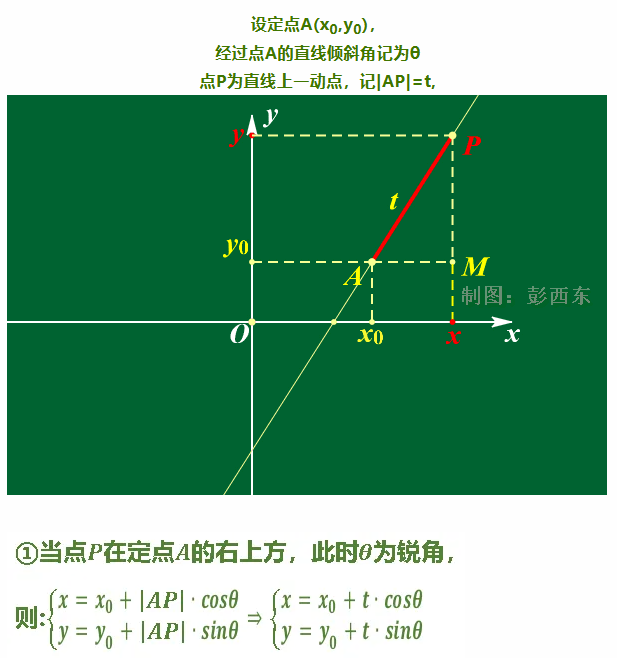
आइए उपरोक्त सूत्र पर ध्यान केंद्रित करें।

जैसा कि ऊपर चित्र में दिखाया गया है, जिस सीधी रेखा से हम परिचित हैं, उसे दूसरे परिप्रेक्ष्य से समझा जा सकता है: t (यानी, बिंदु P से ज्ञात बिंदु (x0,y0) तक |AP| की लंबाई) का उपयोग करते हुए, तब बिंदु P को उपरोक्त त्रिकोणमितीय कार्यों के माध्यम से निर्धारित किया जा सकता है।

अधिक सामान्यतः, इसे इस प्रकार लिखा जा सकता है:

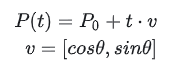
यहां, P0 वेक्टर है [x0,y0]और v भी एक वेक्टर है। जब एक साथ जोड़ा जाता है, तो P(t) वेक्टर [x,y] होता है।

वृत्त को फिर से देख रहे हैं:

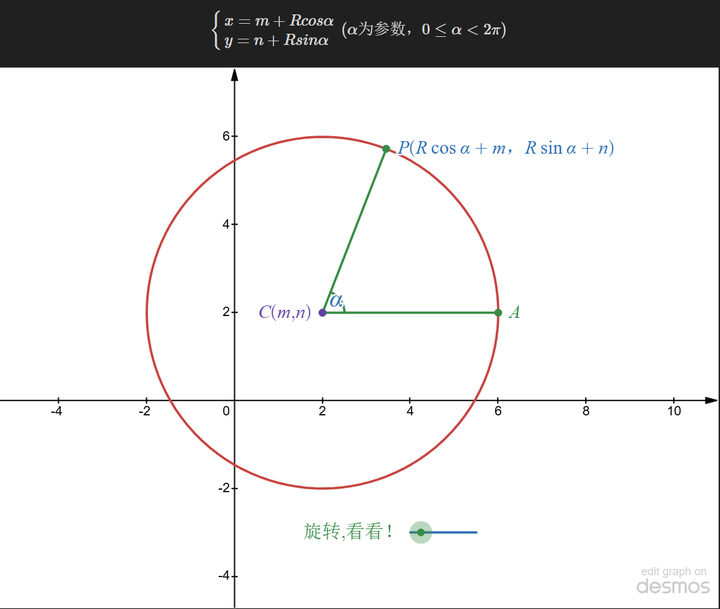
जैसा कि चित्र में दिखाया गया है, वृत्त को एक ज्ञात केंद्र के रूप में देखा जा सकता है, वृत्त पर कोई भी बिंदु घूर्णन कोण और त्रिज्या द्वारा निर्धारित किया जाता है। इसे इस प्रकार भी लिखा जा सकता है:

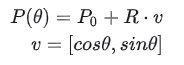
पैरामीट्रिक समीकरण ज्यामितीय अपरिवर्तनीयता बनाए रखते हैं और वृत्त जैसी आकृतियों का प्रतिनिधित्व कर सकते हैं (जहां एक x एकाधिक y मानों से मेल खाता है)।

डी कैस्टेलजौ

डी कैस्टेलजौ एल्गोरिदम एक ऐसी विधि है जिसका उपयोग व्यावहारिक अनुप्रयोगों में ड्राइंग और अन्य कार्यों के लिए बेज़ियर वक्रों का मूल्यांकन और अनुमान लगाने के लिए किया जाता है। पिछली परिभाषा-आधारित मूल्यांकन पद्धति की तुलना में, यह तेज़ और अधिक स्थिर है, और बेज़ियर वक्रों की विशेषताओं के करीब है।

यहां, हम दो लेखों का संदर्भ देते हैं: लिंक1 और लिंक2

सबसे पहले, निम्नलिखित को परिभाषित किया गया है:

उपरोक्त β को देखें। सुपरस्क्रिप्ट और सबस्क्रिप्ट को लेकर यह थोड़ा भ्रमित करने वाला है; आप समझने के लिए निम्नलिखित त्रिकोणीय पुनरावर्तन का उपयोग कर सकते हैं:

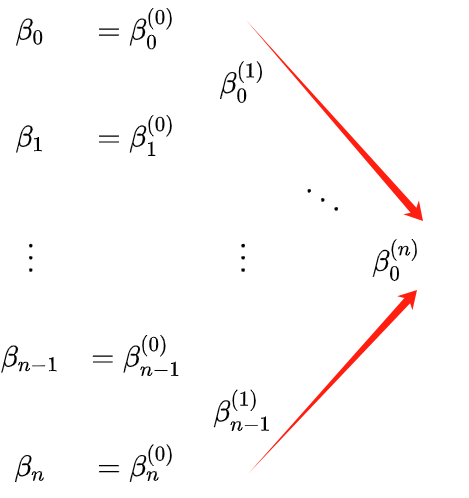
उपरोक्त चित्र में त्रिभुज के लाल किनारे t0 द्वारा विभाजित दो खंडों के नियंत्रण बिंदु हैं। t0, P(t0) को अधिक स्पष्ट रूप से समझने के लिए, ${\beta }_0^{(n)}$β0(n)​ ）, दो वक्रों के नियंत्रण बिंदु, आप निम्न चित्र देख सकते हैं:

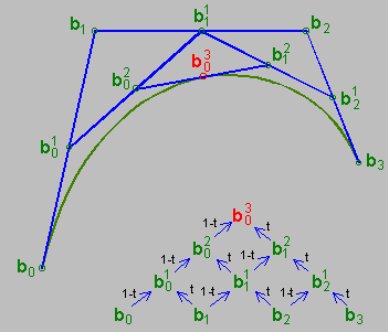
उपरोक्त चित्र विभिन्न बिंदुओं के बीच संबंधों को दर्शाता है जब t=0.5।

"इंटरपोलेशन" के परिप्रेक्ष्य से, गणना प्रक्रिया को इस प्रकार भी समझा जा सकता है:

1. आसन्न नियंत्रण बिंदुओं की प्रत्येक जोड़ी के मध्यबिंदु ढूँढना (क्योंकि t=0.5), यानी, b01, b11, b21 (कृपया मेरे नोटेशन को क्षमा करें; LaTeX में लिखना बहुत परेशानी भरा है)
2. b01−b11 पर मध्यबिंदु b02 ढूंढें, और b11-b21 पर मध्यबिंदु b12 ढूंढें
3. b02−b12 पर मध्यबिंदु b03 खोजें ​ वास्तव में, डी कास्टेलजौ एल्गोरिथ्म का सार प्रक्षेप और पुनरावृत्ति है।

डी कास्टेलजौ पर आधारित वक्र रेखांकन

वर्तमान में, दो विधियाँ देखी गई हैं।

एक विधि में छोटे चरण वृद्धि के साथ 0 से 1 तक ट्रैवर्सिंग शामिल है (यानी। 0.01). हर बार जब P(t) मांगा जाता है, तो निर्धारित करने के लिए एक पुनरावर्ती सूत्र का उपयोग किया जाता है ${\beta }_0^{(n)}$β0(n)​ .

अन्य विधि में P(t=0.5) की तलाश शामिल है, और फिर दो विभाजित वक्रों के लिए, क्रमशः P(t=0.5) की मांग की जाती है... यह उपखंड तब तक जारी रहता है जब तक कि वक्र अनुमानित न हो जाए।

कार्यान्वयन

बिना अभ्यास के सिर्फ देखना हमेशा अवास्तविक लगता है।

इसलिए मैंने कर्व ड्राइंग के लिए अपना स्वयं का कार्यान्वयन कोड लिखा और इसे एक टूलकिट में व्यवस्थित किया: कंपाइलिफ़्स टूलकिट

संबंधित कोर कोड यहां है