परिचय 1

वह प्रक्रिया जिसमें कोई फ़ंक्शन स्वयं को कॉल करता है उसे रिकर्सन कहा जाता है और
संबंधित फ़ंक्शन को पुनरावर्ती फ़ंक्शन कहा जाता है।
चूँकि कंप्यूटर प्रोग्रामिंग गणित का एक मौलिक अनुप्रयोग है, इसलिए आइए
सबसे पहले हम प्रत्यावर्तन के पीछे के गणितीय तर्क को समझने का प्रयास करें।
सामान्यतः हम सभी कार्यों की अवधारणा से परिचित हैं। संक्षेप में, फ़ंक्शन हैं
गणितीय समीकरण जो इनपुट प्रदान करते समय आउटपुट उत्पन्न करते हैं। उदाहरण के लिए:
मान लीजिए कि फ़ंक्शन F(x) एक फ़ंक्शन है जिसे परिभाषित किया गया है: F(x) = x^2 4
हम इस फ़ंक्शन के लिए जावा कोड इस प्रकार लिख सकते हैं:

सार्वजनिक स्थैतिक int F(int x){
वापसी (x * x 4);
}

अब, हम इस फ़ंक्शन में x के विभिन्न मान पास कर सकते हैं और अपना आउटपुट प्राप्त कर सकते हैं
इसलिए।
प्रत्यावर्तन पर आगे बढ़ने से पहले, आइए एक और गणितीय समझने का प्रयास करें
अवधारणा को गणितीय प्रेरण का सिद्धांत (पीएमआई) के रूप में जाना जाता है।

गणितीय प्रेरण का सिद्धांत (पीएमआई) एक कथन को सिद्ध करने की एक तकनीक है, a
सूत्र, या एक प्रमेय जो प्राकृतिक संख्याओं के एक सेट के बारे में दावा किया गया है। इसमें
है निम्नलिखित तीन चरण:
1.** तुच्छ मामले का चरण*: इस चरण में, हम
के लिए वांछित कथन सिद्ध करेंगे n = 0 या n = 1 जैसा आधार मामला।
2.*धारणा का चरण**: इस चरण में, हम मान लेंगे कि वांछित कथन
n = k के लिए मान्य है।

1. चरण को सिद्ध करने के लिए: अनुमान चरण के परिणामों से, हम यह सिद्ध करेंगे कि, n = k 1 वांछित समीकरण के लिए भी सत्य है जब भी n = k सत्य है।

उदाहरण के लिए: आइए गणितीय प्रेरण के सिद्धांत का उपयोग करके साबित करें कि:
एस(एन): 1 2 3 ... एन = (एन * (एन 1))/2
(प्रथम N प्राकृतिक संख्याओं का योग)
सबूत:
चरण 1: N = 1 के लिए, S(1) = 1 सत्य है।
चरण 2: मान लें, दिया गया कथन N = k के लिए सत्य है, अर्थात,
1 2 3 .... के = (के * (के 1))/2
चरण 3: आइए चरण 2 का उपयोग करके N = k 1 के लिए कथन को सिद्ध करें।

साबित करने के लिए: 1 2 3 ... (के 1) = ((के 1)*(के 2))/2
सबूत:

चरण 2 पर प्राप्त परिणाम में एलएचएस और आरएचएस दोनों में (के 1) जोड़ना:
1 2 3 ... (के 1) = (के*(के 1))/2 (के 1)

अब, RHS की ओर से सामान्य (k 1) लेते हुए:
1 2 3 ... (के 1) = (के 1)*((के 2)/2)

उस बयान के अनुसार जिसे हम साबित करने की कोशिश कर रहे हैं:
1 2 3 ... (के 1) = ((के 1)*(के 2))/2
अत: सिद्ध हुआ।

प्रत्यावर्तन का कार्य

हम उपरोक्त तीन को सारांशित करके पुनरावर्ती दृष्टिकोण के चरणों को परिभाषित कर सकते हैं
चरण:
● बेस केस: एक पुनरावर्ती फ़ंक्शन में एक समापन स्थिति होनी चाहिए जिस पर
प्रक्रिया स्वयं कॉल करना बंद कर देगी. ऐसे मामले को आधार मामले के रूप में जाना जाता है। बेस केस के बिना, यह स्वयं कॉल करता रहेगा और
में फंस जाएगा अनंत लूप। जल्द ही, रिकर्सन गहराई* पार हो जाएगी और यह फेंक देगा
एक गलती।
● पुनरावर्ती कॉल: पुनरावर्ती फ़ंक्शन स्वयं को छोटे संस्करण पर लागू करेगा
मुख्य समस्या का. इस चरण को लिखते समय हमें सावधान रहने की आवश्यकता है क्योंकि यह है
आपकी छोटी समस्या क्या है, इसका सही-सही पता लगाना महत्वपूर्ण है।
● छोटी गणना: आम तौर पर, हम प्रत्येक पुनरावर्ती में एक गणना चरण निष्पादित करते हैं
पुकारना। हम इस गणना चरण को पुनरावर्ती कॉल से पहले या बाद में प्राप्त कर सकते हैं
समस्या की प्रकृति के आधार पर।

नोट: रिकर्सन एक इन-बिल्ट स्टैक का उपयोग करता है जो रिकर्सिव कॉल को संग्रहीत करता है। इसलिए,
मेमोरी अतिप्रवाह से बचने के लिए पुनरावर्ती कॉलों की संख्या यथासंभव कम होनी चाहिए। अगर
रिकर्सन कॉल की संख्या अधिकतम स्वीकार्य राशि से अधिक है,
**प्रत्यावर्तन गहराई** पार हो जाएगी।
अब, आइए देखें कि रिकर्सन का उपयोग करके कुछ सामान्य समस्याओं को कैसे हल किया जाए

समस्या विवरण - किसी संख्या का गुणनखंड ज्ञात करें

दृष्टिकोण: पीएमआई के तीन चरणों का पता लगाना और फिर उसका उपयोग करके संबंधित करना
प्रत्यावर्तन

1. प्रेरण चरण: किसी संख्या n - F(n) के फैक्टोरियल की गणना करना प्रेरण परिकल्पना: हमने पहले ही n-1 - F(n-1)
का फैक्टोरियल प्राप्त कर लिया है।
2. F(n) को F(n-1) के रूप में व्यक्त करना: F(n)=n*F(n-1). इस प्रकार हमें
मिलता है

सार्वजनिक स्थैतिक पूर्णांक तथ्य(पूर्णांक n){
int ans = तथ्य(n-1); #धारणा चरण
वापसी उत्तर*एन; #धारणा चरण से समस्या का समाधान
}

1. कोड अभी भी पूरा नहीं हुआ है। लुप्त भाग आधार मामला है। अब हम करेंगे उस स्थिति का पता लगाने के लिए ड्राई रन करें जहां रिकर्सन को रोकने की आवश्यकता है। n = 5 पर विचार करें:

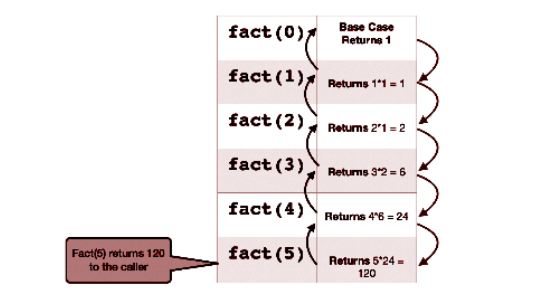
जैसा कि हम ऊपर देख सकते हैं, हम पहले से ही n = 0 का उत्तर जानते हैं, जो 1 है। इसलिए हम करेंगे
इसे हमारे आधार मामले के रूप में रखें। इसलिए, कोड अब बन जाता है:

पब्लिक स्टेटिक इंट फैक्टोरियल(इंट एन){
अगर (एन == 0) // बेस केस
वापसी 1;
अन्य
वापसी n*फैक्टोरियल(n-1); // पुनरावर्ती मामला
}