k-निकटतम पड़ोसी प्रतिगमन

के-निकटतम पड़ोसी (के-एनएन) प्रतिगमन एक गैर-पैरामीट्रिक विधि है जो फीचर स्पेस में के-निकटतम प्रशिक्षण डेटा बिंदुओं के औसत (या भारित औसत) के आधार पर आउटपुट मूल्य की भविष्यवाणी करता है। यह दृष्टिकोण किसी विशिष्ट कार्यात्मक रूप को ग्रहण किए बिना डेटा में जटिल संबंधों को प्रभावी ढंग से मॉडल कर सकता है।

के-एनएन प्रतिगमन विधि को निम्नानुसार संक्षेपित किया जा सकता है:

1. दूरी मीट्रिक: डेटा बिंदुओं की "निकटता" निर्धारित करने के लिए एल्गोरिदम एक दूरी मीट्रिक (आमतौर पर यूक्लिडियन दूरी) का उपयोग करता है।
2. k पड़ोसी: पैरामीटर k निर्दिष्ट करता है कि भविष्यवाणी करते समय कितने निकटतम पड़ोसियों पर विचार किया जाए।
3. भविष्यवाणी: एक नए डेटा बिंदु के लिए अनुमानित मूल्य उसके निकटतम पड़ोसियों के मूल्यों का औसत है।

महत्वपूर्ण अवधारणाएं

1. गैर-पैरामीट्रिक: पैरामीट्रिक मॉडल के विपरीत, के-एनएन इनपुट सुविधाओं और लक्ष्य चर के बीच अंतर्निहित संबंध के लिए एक विशिष्ट रूप नहीं मानता है। यह इसे जटिल पैटर्न कैप्चर करने में लचीला बनाता है।

2. दूरी गणना: दूरी मीट्रिक का चुनाव मॉडल के प्रदर्शन को महत्वपूर्ण रूप से प्रभावित कर सकता है। सामान्य मेट्रिक्स में यूक्लिडियन, मैनहट्टन और मिन्कोव्स्की दूरियाँ शामिल हैं।

3. k की पसंद: पड़ोसियों की संख्या (k) को क्रॉस-वैलिडेशन के आधार पर चुना जा सकता है। एक छोटा k ओवरफिटिंग का कारण बन सकता है, जबकि एक बड़ा k पूर्वानुमान को बहुत अधिक सुचारू कर सकता है, संभावित रूप से अंडरफिटिंग।

k-निकटतम पड़ोसी प्रतिगमन उदाहरण

यह उदाहरण दर्शाता है कि के-एनएन की गैर-पैरामीट्रिक प्रकृति का लाभ उठाते हुए जटिल संबंधों को मॉडल करने के लिए बहुपद विशेषताओं के साथ के-एनएन प्रतिगमन का उपयोग कैसे किया जाए।

पायथन कोड उदाहरण

1. आयात पुस्तकालय

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

यह ब्लॉक डेटा हेरफेर, प्लॉटिंग और मशीन लर्निंग के लिए आवश्यक लाइब्रेरी आयात करता है।

2. नमूना डेटा उत्पन्न करें

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

यह ब्लॉक वास्तविक दुनिया डेटा विविधताओं का अनुकरण करते हुए, कुछ शोर के साथ संबंध का प्रतिनिधित्व करने वाला नमूना डेटा उत्पन्न करता है।

3. डेटासेट को विभाजित करें

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

यह ब्लॉक मॉडल मूल्यांकन के लिए डेटासेट को प्रशिक्षण और परीक्षण सेट में विभाजित करता है।

4. बहुपद विशेषताएँ बनाएँ

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

यह ब्लॉक प्रशिक्षण और परीक्षण डेटासेट से बहुपद विशेषताएं उत्पन्न करता है, जिससे मॉडल को गैर-रेखीय संबंधों को पकड़ने की अनुमति मिलती है।

5. के-एनएन रिग्रेशन मॉडल बनाएं और प्रशिक्षित करें

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

यह ब्लॉक k-NN प्रतिगमन मॉडल को आरंभ करता है और प्रशिक्षण डेटासेट से प्राप्त बहुपद सुविधाओं का उपयोग करके इसे प्रशिक्षित करता है।

6. भविष्यवाणी करें

y_pred = knn_model.predict(X_poly_test)

यह ब्लॉक परीक्षण सेट पर पूर्वानुमान लगाने के लिए प्रशिक्षित मॉडल का उपयोग करता है।

7. परिणाम प्लॉट करें

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

यह ब्लॉक फिट किए गए वक्र की कल्पना करते हुए, के-एनएन रिग्रेशन मॉडल से अनुमानित मूल्यों की तुलना में वास्तविक डेटा बिंदुओं का एक स्कैटर प्लॉट बनाता है।

के = 1 के साथ आउटपुट:

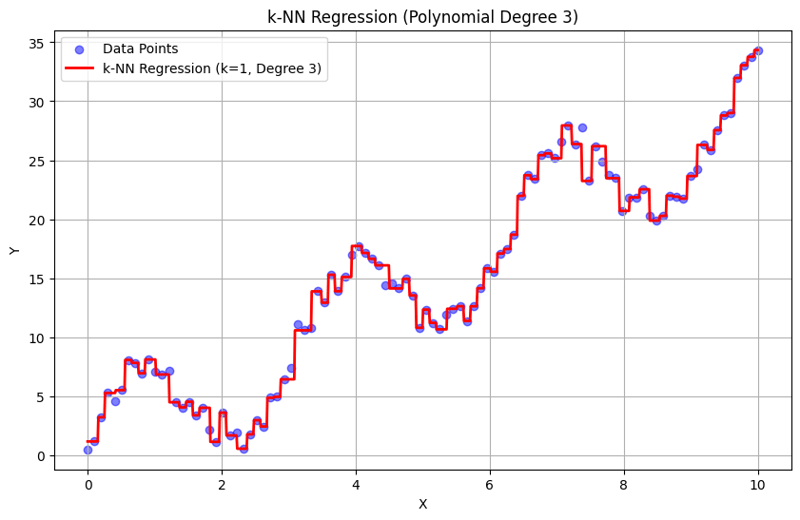
के = 10 के साथ आउटपुट:

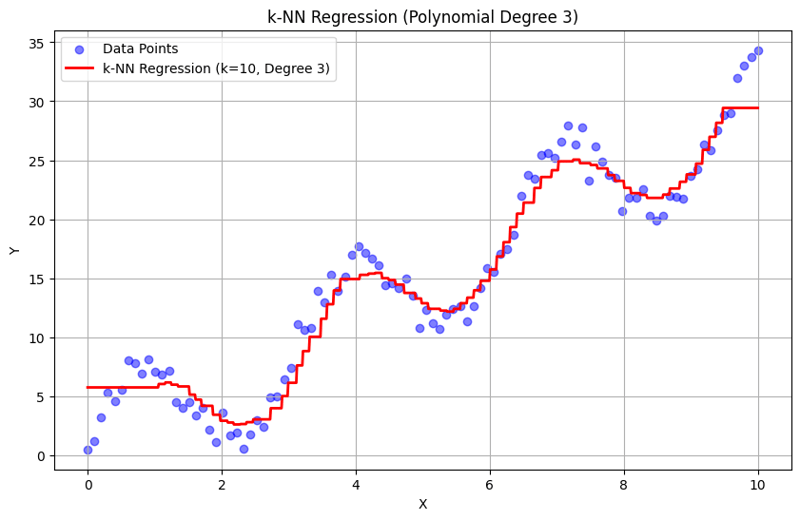
यह संरचित दृष्टिकोण दर्शाता है कि बहुपद विशेषताओं के साथ के-निकटतम पड़ोसी प्रतिगमन को कैसे कार्यान्वित और मूल्यांकन किया जाए। आस-पास के पड़ोसियों की प्रतिक्रियाओं के औसत के माध्यम से स्थानीय पैटर्न को कैप्चर करके, के-एनएन प्रतिगमन एक सीधा कार्यान्वयन प्रदान करते हुए डेटा में जटिल संबंधों को प्रभावी ढंग से मॉडल करता है। K और बहुपद डिग्री का चुनाव अंतर्निहित रुझानों को पकड़ने में मॉडल के प्रदर्शन और लचीलेपन को महत्वपूर्ण रूप से प्रभावित करता है।