जैसा कि हम विभिन्न सॉर्टिंग एल्गोरिदम के बारे में बात कर रहे हैं, आज हम चयन सॉर्ट एल्गोरिदम के बारे में सीखेंगे। एक सॉर्टिंग एल्गोरिदम जो मेमोरी-बाधित वातावरण में संभावित न्यूनतम मात्रा में स्वैप की अनुमति देता है।

विषयसूची

1. परिचय
2. चयन सॉर्ट एल्गोरिदम क्या है?
3. चयन सॉर्ट कैसे काम करता है?
   • समय जटिलता
   • अंतरिक्ष जटिलता
4. जावास्क्रिप्ट में कार्यान्वयन
5. लीटकोड समस्याओं का समाधान
6. निष्कर्ष

परिचय

चयन सॉर्ट एक सरल लेकिन प्रभावी सॉर्टिंग एल्गोरिदम है जो सूची के अनसोल्ड भाग से सबसे छोटे (या सबसे बड़े) तत्व को बार-बार चुनकर और सॉर्ट किए गए भाग की शुरुआत (या अंत) में ले जाकर काम करता है। यह प्रक्रिया तब तक दोहराई जाती है जब तक कि पूरी सूची क्रमबद्ध न हो जाए। इस लेख में, हम चयन सॉर्ट एल्गोरिथ्म, जावास्क्रिप्ट में इसके कार्यान्वयन और वास्तविक दुनिया की समस्याओं को हल करने में इसके अनुप्रयोगों के विवरण पर चर्चा करेंगे।

चयन सॉर्ट एल्गोरिथम क्या है?

चयन सॉर्ट एल्गोरिदम एक इन-प्लेस तुलना सॉर्टिंग एल्गोरिदम है। यह इनपुट सूची को दो भागों में विभाजित करता है:

1. बाएं छोर पर क्रमबद्ध भाग
2. दाईं ओर का अवर्गीकृत भाग

एल्गोरिदम बार-बार अवर्गीकृत भाग से सबसे छोटे तत्व का चयन करता है और इसे सबसे बाएं अवर्गीकृत तत्व के साथ स्वैप करता है, क्रमबद्ध और अवर्गीकृत भागों के बीच की सीमा को एक तत्व से दाईं ओर ले जाता है।

चयन सॉर्ट कैसे काम करता है?

आइए सरणी का उपयोग करके एक उदाहरण देखें [64, 25, 12, 22, 11]:

1. प्रारंभिक सरणी: [64, 25, 12, 22, 11]

• क्रमबद्ध भाग: []
• अवर्गीकृत भाग: [64, 25, 12, 22, 11]

1. पहला पास:

• बिना क्रमित भाग में न्यूनतम खोजें: 11
• पहले अवर्गीकृत तत्व के साथ 11 स्वैप करें (64)
• परिणाम: [11, 25, 12, 22, 64]
• क्रमबद्ध भाग: [11]
• अवर्गीकृत भाग: [25, 12, 22, 64]

1. दूसरा पास:

• बिना छांटे गए हिस्से में न्यूनतम खोजें: 12
• पहले अवर्गीकृत तत्व के साथ 12 स्वैप करें (25)
• परिणाम: [11, 12, 25, 22, 64]
• क्रमबद्ध भाग: [11, 12]
• अवर्गीकृत भाग: [25, 22, 64]

1. तीसरी पास:

• बिना छांटे गए हिस्से में न्यूनतम खोजें: 22
• पहले अवर्गीकृत तत्व के साथ 22 स्वैप करें (25)
• परिणाम: [11, 12, 22, 25, 64]
• क्रमबद्ध भाग: [11, 12, 22]
• अवर्गीकृत भाग: [25, 64]

1. चौथी पास:

• बिना छांटे गए हिस्से में न्यूनतम खोजें: 25
• 25 पहले से ही सही स्थिति में है
• परिणाम: [11, 12, 22, 25, 64]
• क्रमबद्ध भाग: [11, 12, 22, 25]
• अवर्गीकृत भाग: [64]

1. अंतिम पास:
   • केवल एक तत्व बचा है, यह स्वचालित रूप से सही स्थिति में है
   • अंतिम परिणाम: [11, 12, 22, 25, 64]

सरणी अब पूरी तरह से क्रमबद्ध है।

समय की जटिलता

चयन सॉर्ट में सभी मामलों (सर्वोत्तम, औसत और सबसे खराब) में O(n^2) की समय जटिलता होती है, जहां n सरणी में तत्वों की संख्या है। यह है क्योंकि:

• बाहरी लूप n-1 बार चलता है
• बाहरी लूप के प्रत्येक पुनरावृत्ति के लिए, आंतरिक लूप n-i-1 बार चलता है (जहां i बाहरी लूप का वर्तमान पुनरावृत्ति है)

इसके परिणामस्वरूप लगभग (n^2)/2 तुलनाएं और n स्वैप होते हैं, जो O(n^2) को सरल बनाता है।

इस द्विघात समय जटिलता के कारण, चयन सॉर्ट बड़े डेटासेट के लिए कुशल नहीं है। हालाँकि, इसकी सरलता और यह तथ्य कि यह न्यूनतम संभव संख्या में स्वैप करता है, इसे कुछ स्थितियों में उपयोगी बना सकता है, खासकर जब सहायक मेमोरी सीमित है।

अंतरिक्ष जटिलता

सिलेक्शन सॉर्ट में O(1) की स्पेस जटिलता होती है क्योंकि यह एरे को उसी स्थान पर सॉर्ट करता है। इसमें इनपुट आकार की परवाह किए बिना केवल अतिरिक्त मेमोरी स्पेस की निरंतर मात्रा की आवश्यकता होती है। यह इसे मेमोरी-कुशल बनाता है, जो मेमोरी-बाधित वातावरण में फायदेमंद हो सकता है।

जावास्क्रिप्ट में कार्यान्वयन

यहां चयन सॉर्ट एल्गोरिदम का जावास्क्रिप्ट कार्यान्वयन है:

function selectionSort(arr) {
  const n = arr.length;

  for (let i = 0; i 


आइए कोड को तोड़ें:

हम एक फ़ंक्शन चयन सॉर्ट को परिभाषित करते हैं जो एक सरणी को इनपुट के रूप में लेता है।
हम बाहरी लूप (i) के साथ सरणी के माध्यम से पुनरावृति करते हैं, जो क्रमबद्ध और अवर्गीकृत भागों के बीच की सीमा का प्रतिनिधित्व करता है।
प्रत्येक पुनरावृत्ति के लिए, हम मानते हैं कि पहला अवर्गीकृत तत्व न्यूनतम है और उसके सूचकांक को संग्रहीत करता है।
फिर हम अवर्गीकृत हिस्से में वास्तविक न्यूनतम तत्व खोजने के लिए एक आंतरिक लूप (जे) का उपयोग करते हैं।
यदि हमें कोई छोटा तत्व मिलता है, तो हम minIndex को अपडेट करते हैं।
न्यूनतम खोजने के बाद, यदि आवश्यक हो तो हम इसे पहले अवर्गीकृत तत्व के साथ स्वैप करते हैं।
हम इस प्रक्रिया को तब तक दोहराते हैं जब तक कि संपूर्ण सरणी क्रमबद्ध न हो जाए।

  
  
  लीटकोड समस्याओं का समाधान


आइए चयन सॉर्ट एल्गोरिदम का उपयोग करके एक लेटकोड एल्गोरिदम समस्या को हल करें। क्या हम?

  
  
  समस्या: एक सरणी को क्रमबद्ध करें [मध्यम]


समस्या: पूर्णांक संख्याओं की एक सरणी को देखते हुए, सरणी को आरोही क्रम में क्रमबद्ध करें और इसे वापस कर दें। आपको O(nlog(n)) समय जटिलता में किसी भी अंतर्निहित फ़ंक्शन का उपयोग किए बिना और यथासंभव न्यूनतम स्थान जटिलता के साथ समस्या का समाधान करना होगा।

दृष्टिकोण:: इस समस्या को हल करने के लिए, हम सीधे चयन सॉर्ट एल्गोरिदम लागू कर सकते हैं। इसमें सरणी के माध्यम से पुनरावृत्ति करना, अवर्गीकृत भाग में सबसे छोटा तत्व ढूंढना और इसे पहले अवर्गीकृत तत्व के साथ स्वैप करना शामिल है। हम इस प्रक्रिया को तब तक दोहराते हैं जब तक कि संपूर्ण सरणी क्रमबद्ध न हो जाए।

समाधान:

// This function sorts an array of integers in ascending order using the Selection Sort algorithm.
const sortArray = function (nums) {
  // Get the length of the input array.
  const n = nums.length;

  // Iterate through the array, starting from the first element.
  for (let i = 0; i 


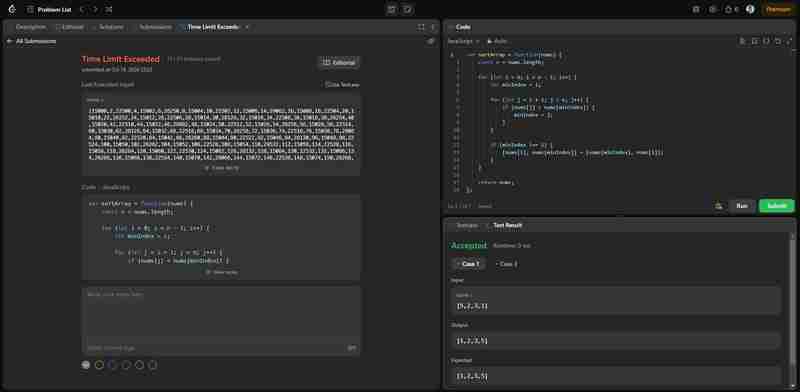
यह समाधान सीधे उस चयन सॉर्ट एल्गोरिदम को लागू करता है जिसे हमने पहले लागू किया था। हालाँकि यह समस्या को सही ढंग से हल करता है, यह ध्यान देने योग्य है कि यह समाधान चयन सॉर्ट की O(n^2) समय जटिलता के कारण लीटकोड पर बड़े इनपुट के लिए समय सीमा को पार कर सकता है। नीचे दी गई छवि दिखाती है कि समाधान सही है लेकिन कुशल नहीं है।



  
  
  निष्कर्ष


निष्कर्ष रूप में, सिलेक्शन सॉर्ट एक सरल और सहज सॉर्टिंग एल्गोरिदम है जो सॉर्टिंग तकनीकों की दुनिया के लिए एक उत्कृष्ट परिचय के रूप में कार्य करता है। इसकी सरलता इसे समझना और लागू करना आसान बनाती है, जिससे यह शुरुआती लोगों के लिए एक मूल्यवान शिक्षण उपकरण बन जाता है। हालाँकि, इसकी द्विघात समय जटिलता O(n^2) के कारण, यह बड़े डेटासेट के लिए कुशल नहीं है। बड़े डेटासेट या प्रदर्शन-महत्वपूर्ण अनुप्रयोगों के लिए, क्विकसॉर्ट, मर्जसॉर्ट या अंतर्निहित सॉर्टिंग फ़ंक्शन जैसे अधिक कुशल एल्गोरिदम को प्राथमिकता दी जाती है।


  
  
  अपडेट और कनेक्टेड रहें


यह सुनिश्चित करने के लिए कि आप इस श्रृंखला का कोई भी भाग न चूकें और अधिक गहराई के लिए मेरे साथ जुड़ें

सॉफ्टवेयर डेवलपमेंट (वेब, सर्वर, मोबाइल या स्क्रैपिंग/ऑटोमेशन), डेटा पर चर्चा

संरचनाओं और एल्गोरिदम, और अन्य रोमांचक तकनीकी विषयों पर मेरा अनुसरण करें:



    
      

        
    
  

    

महान समाधान?फ़ॉलो करें

    

      सॉफ्टवेयर इंजीनियर | तकनीकी लेखक | बैकएंड, वेब और मोबाइल डेवलपर? | कुशल और स्केलेबल सॉफ़्टवेयर समाधान तैयार करने का जुनून। #लेट्सकनेक्ट?
    
  

• गिटहब
• लिंक्डइन
• एक्स (ट्विटर)

बने रहें और खुश रहें कोडिंग ?‍??