जब डेवलपर्स पहली बार इस आश्चर्यजनक परिणाम का सामना करते हैं तो जावास्क्रिप्ट का अक्सर उपहास किया जाता है:

0.1   0.2 == 0.30000000000000004

जावास्क्रिप्ट द्वारा संख्याओं को संभालने के बारे में मीम्स व्यापक हैं, जो अक्सर कई लोगों को यह विश्वास दिलाते हैं कि यह व्यवहार भाषा के लिए अद्वितीय है।

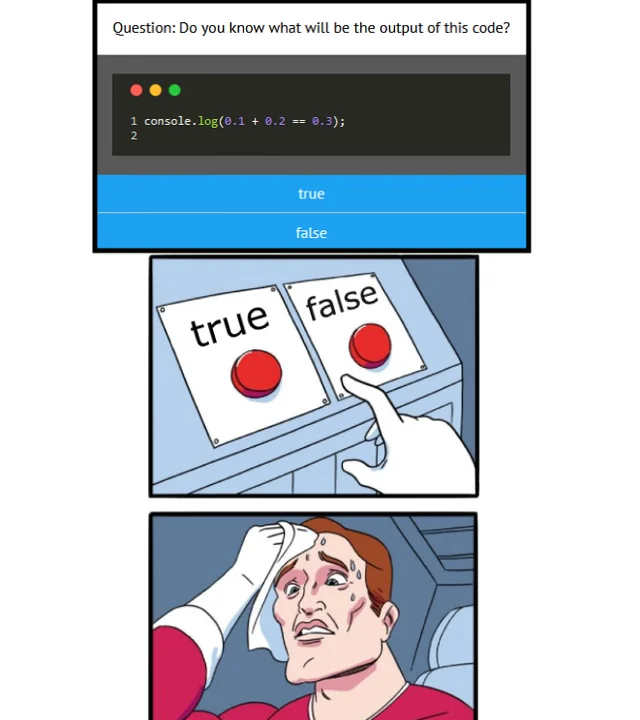
हालाँकि, यह विचित्रता केवल जावास्क्रिप्ट तक ही सीमित नहीं है। यह इस बात का परिणाम है कि अधिकांश प्रोग्रामिंग भाषाएं फ़्लोटिंग-पॉइंट अंकगणित को कैसे संभालती हैं।

उदाहरण के लिए, यहां Java और Go के कोड स्निपेट हैं जो समान परिणाम देते हैं:

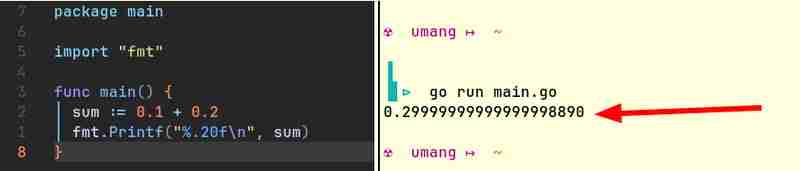
कंप्यूटर मूल रूप से केवल पूर्णांक संग्रहीत कर सकते हैं। वे भिन्नों को नहीं समझते. (वे कैसे करेंगे? कंप्यूटर अंकगणित करने का एकमात्र तरीका कुछ लाइटों को चालू या बंद करना है। प्रकाश या तो चालू या बंद हो सकता है। यह "आधा" चालू नहीं हो सकता है!) उन्हें फ़्लोटिंग पॉइंट संख्याओं का प्रतिनिधित्व करने का कोई तरीका चाहिए . चूँकि यह प्रतिनिधित्व पूरी तरह से सटीक नहीं है, अक्सर, 0.1 0.2 0.3 के बराबर नहीं होता है।

सभी भिन्न जिनके हर संख्या प्रणाली के आधार के अभाज्य गुणनखंडों से बने होते हैं, उन्हें स्पष्ट रूप से व्यक्त किया जा सकता है जबकि किसी अन्य भिन्न में दोहराए जाने वाले दशमलव होंगे। उदाहरण के लिए, आधार 10 वाली संख्या प्रणाली में, 1/2, 1/4, 1/5, 1/10 जैसे भिन्नों को स्पष्ट रूप से दर्शाया जाता है क्योंकि प्रत्येक मामले में हर 2 या 5 से बने होते हैं - 10 के अभाज्य गुणनखंड हालाँकि, 1/3, 1/6, 1/7 जैसे भिन्नों में आवर्ती दशमलव होते हैं।

इसी तरह, बाइनरी सिस्टम में 1/2, 1/4, 1/8 जैसे अंशों को स्पष्ट रूप से व्यक्त किया जाता है जबकि अन्य सभी अंशों में आवर्ती दशमलव होते हैं। जब आप इन आवर्ती दशमलवों पर अंकगणित करते हैं, तो आपके पास बचे हुए अंक रह जाते हैं जो कंप्यूटर के संख्याओं के बाइनरी प्रतिनिधित्व को मानव पठनीय आधार -10 प्रतिनिधित्व में परिवर्तित करने पर आगे बढ़ जाते हैं। इसी से लगभग सही परिणाम प्राप्त होते हैं।

अब जब हमने यह स्थापित कर लिया है कि यह समस्या केवल जावास्क्रिप्ट के लिए नहीं है, तो आइए जानें कि यह व्यवहार क्यों होता है यह समझने के लिए फ्लोटिंग-पॉइंट संख्याओं को हुड के नीचे कैसे दर्शाया और संसाधित किया जाता है।

यह समझने के लिए कि फ्लोटिंग पॉइंट नंबरों को हुड के नीचे कैसे दर्शाया और संसाधित किया जाता है, हमें पहले आईईईई 754 फ्लोटिंग पॉइंट मानक को समझना होगा।

आईईईई 754 मानक कंप्यूटर सिस्टम में फ्लोटिंग-पॉइंट नंबरों पर अंकगणित का प्रतिनिधित्व करने और प्रदर्शन करने के लिए व्यापक रूप से उपयोग किया जाने वाला विनिर्देश है। इसे विभिन्न कंप्यूटिंग प्लेटफ़ॉर्म पर फ़्लोटिंग-पॉइंट अंकगणित का उपयोग करते समय स्थिरता की गारंटी देने के लिए बनाया गया था। अधिकांश प्रोग्रामिंग भाषाएं और हार्डवेयर कार्यान्वयन (सीपीयू, जीपीयू, आदि) इस मानक का पालन करते हैं।

इस प्रकार एक संख्या को IEEE 754 प्रारूप में दर्शाया जाता है:

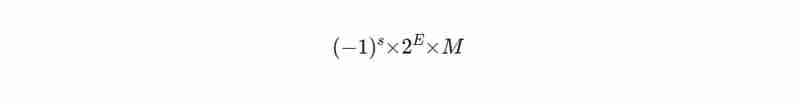
यहां s साइन बिट है (सकारात्मक के लिए 0, नकारात्मक के लिए 1), M मंटिसा है (संख्या के अंक रखता है) और E वह घातांक है जो संख्या का पैमाना निर्धारित करता है।

आप एम और ई के लिए कोई पूर्णांक मान नहीं ढूंढ पाएंगे जो इस प्रारूप में 0.1, 0.2 या 0.3 जैसी संख्याओं का सटीक प्रतिनिधित्व कर सके। हम केवल एम और ई के लिए मान चुन सकते हैं जो निकटतम परिणाम देते हैं।

यहां एक उपकरण है जिसका उपयोग आप दशमलव संख्याओं के IEEE 754 नोटेशन निर्धारित करने के लिए कर सकते हैं: https://www.h-schmidt.net/FloatConverter/IEEE754.html

आईईईई 754 0.25 का अंकन:

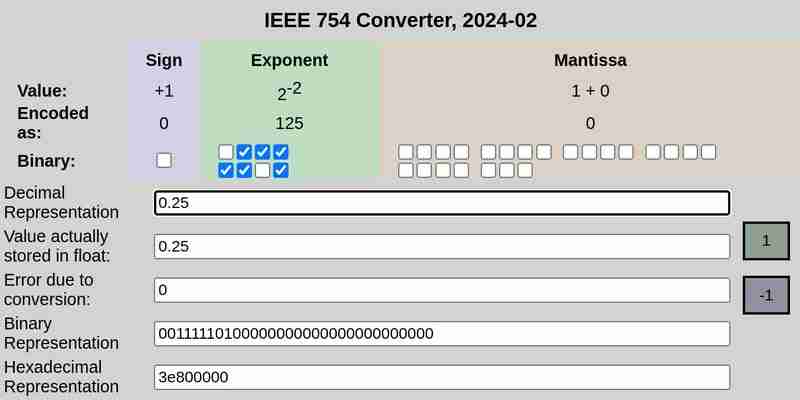
आईईईई 754 क्रमशः 0.1 और 0.2 का अंकन:

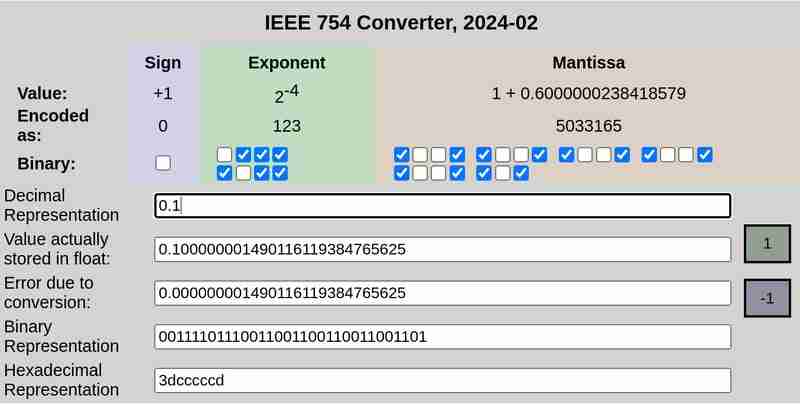
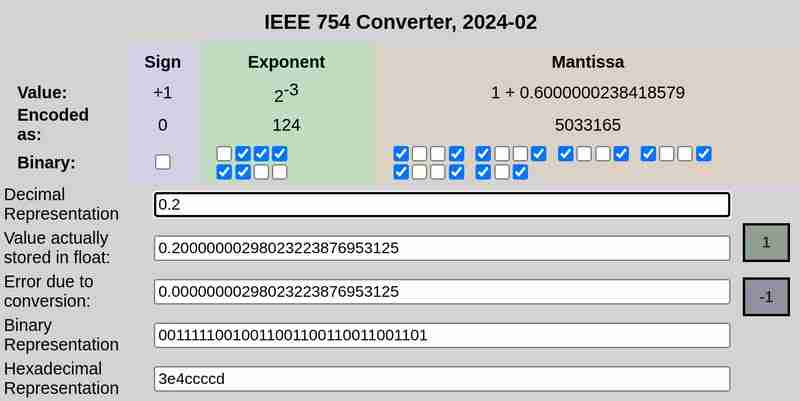
कृपया ध्यान दें कि 0.25 के मामले में रूपांतरण के कारण त्रुटि 0 थी, जबकि 0.1 और 0.2 में गैर-शून्य त्रुटियां थीं।

आईईईई 754 फ़्लोटिंग-पॉइंट संख्याओं का प्रतिनिधित्व करने के लिए निम्नलिखित प्रारूपों को परिभाषित करता है:

• एकल-परिशुद्धता (32-बिट): संकेत के लिए 1 बिट, घातांक के लिए 8 बिट, मंटिसा के लिए 23 बिट्स

• डबल-प्रिसिजन (64-बिट): साइन के लिए 1 बिट, एक्सपोनेंट के लिए 11 बिट, मंटिसा के लिए 52 बिट्स

सरलता के लिए, आइए एकल-परिशुद्धता प्रारूप पर विचार करें जो 32 बिट्स का उपयोग करता है।

0.1 का 32 बिट प्रतिनिधित्व है:

0 01111011 10011001100110011001101

यहां पहला बिट संकेत का प्रतिनिधित्व करता है (0 जिसका अर्थ इस मामले में सकारात्मक है), अगले 8 बिट्स (01111011) घातांक का प्रतिनिधित्व करते हैं और अंतिम 23 बिट्स (10011001100110011001101) मंटिसा का प्रतिनिधित्व करते हैं।

यह सटीक प्रतिनिधित्व नहीं है। यह प्रतिनिधित्व करता है ≈ 0.100000001490116119384765625

इसी प्रकार, 0.2 का 32 बिट प्रतिनिधित्व है:

0 01111100 10011001100110011001101

यह भी कोई सटीक प्रतिनिधित्व नहीं है। यह प्रतिनिधित्व करता है ≈ 0.20000000298023223876953125

जब जोड़ा जाता है, तो इसका परिणाम होता है:

0 01111101 11001101010011001100110 

जो दशमलव प्रतिनिधित्व में ≈ 0.30000001192092896 है।

निष्कर्ष में, 0.1 0.2 का 0.3 न मिलना प्रतीत होने वाला हैरान करने वाला परिणाम जावास्क्रिप्ट के लिए विशिष्ट विसंगति नहीं है, बल्कि प्रोग्रामिंग भाषाओं में फ्लोटिंग-पॉइंट अंकगणित की सीमाओं का परिणाम है। इस व्यवहार की जड़ें संख्याओं के द्विआधारी प्रतिनिधित्व में निहित हैं, जो स्वाभाविक रूप से कुछ अंशों को संभालते समय सटीक त्रुटियों की ओर ले जाती हैं।