ग्राफ़ एल्गोरिदम का उपयोग करके वास्तविक दुनिया की कई समस्याओं को हल किया जा सकता है। ग्राफ़ मॉडलिंग और वास्तविक दुनिया की समस्याओं को हल करने में उपयोगी होते हैं। उदाहरण के लिए, दो शहरों के बीच उड़ानों की न्यूनतम संख्या खोजने की समस्या को एक ग्राफ का उपयोग करके तैयार किया जा सकता है, जहां कोने शहरों का प्रतिनिधित्व करते हैं और किनारे दो आसन्न शहरों के बीच उड़ानों का प्रतिनिधित्व करते हैं, जैसा कि नीचे चित्र में दिखाया गया है। कनेक्टिंग उड़ानों की न्यूनतम संख्या खोजने की समस्या
दो शहरों के बीच एक ग्राफ़ में दो शीर्षों के बीच सबसे छोटा रास्ता खोजने तक सीमित कर दिया गया है।

ग्राफ समस्याओं के अध्ययन को ग्राफ सिद्धांत के रूप में जाना जाता है। ग्राफ़ सिद्धांत की स्थापना 1736 में लियोनहार्ड यूलर द्वारा की गई थी, जब उन्होंने प्रसिद्ध सेवेन ब्रिजेस ऑफ़ कोनिग्सबर्ग समस्या को हल करने के लिए ग्राफ़ शब्दावली की शुरुआत की थी। कोनिग्सबर्ग शहर, प्रशिया (अब कलिनिनग्राद, रूस), प्रीगेल नदी द्वारा विभाजित किया गया था। नदी पर दो द्वीप थे। शहर और द्वीप सात पुलों से जुड़े हुए थे, जैसा कि नीचे चित्र (ए) में दिखाया गया है। सवाल यह है कि क्या कोई पैदल चल सकता है, प्रत्येक पुल को ठीक एक बार पार कर सकता है और शुरुआती बिंदु पर लौट सकता है? यूलर ने साबित कर दिया कि यह संभव नहीं है।

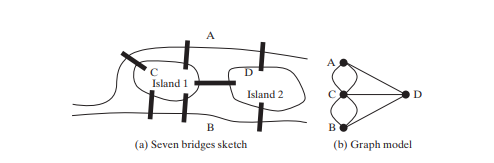
प्रमाण स्थापित करने के लिए, यूलर ने सबसे पहले सभी सड़कों को हटाकर कोनिग्सबर्ग शहर के मानचित्र को अमूर्त किया, चित्र ऊपर (ए) में दिखाए गए स्केच का निर्माण किया। इसके बाद, उन्होंने प्रत्येक भूभाग को एक बिंदु से बदल दिया, जिसे vertex या नोड कहा जाता है, और प्रत्येक पुल को एक रेखा से बदल दिया, जिसे किनारा कहा जाता है, जैसा कि इसमें दिखाया गया है ऊपर चित्र (बी)। शीर्षों और किनारों वाली इस संरचना को ग्राफ कहा जाता है।

ग्राफ़ को देखते हुए, हम पूछते हैं कि क्या कोई पथ है जो किसी शीर्ष से शुरू होता है, सभी किनारों को ठीक एक बार पार करता है, और प्रारंभिक शीर्ष पर लौटता है। यूलर ने सिद्ध किया कि ऐसे पथ के अस्तित्व के लिए, प्रत्येक शीर्ष पर किनारों की संख्या सम होनी चाहिए। इसलिए, कोनिग्सबर्ग के सात पुलों की समस्या का कोई समाधान नहीं है।

ग्राफ़ समस्याओं को अक्सर एल्गोरिदम का उपयोग करके हल किया जाता है। ग्राफ़ एल्गोरिदम के विभिन्न क्षेत्रों में कई अनुप्रयोग हैं, जैसे कंप्यूटर विज्ञान, गणित, जीव विज्ञान, इंजीनियरिंग, अर्थशास्त्र, आनुवंशिकी और सामाजिक विज्ञान।

बुनियादी ग्राफ़ शब्दावली

एक ग्राफ़ में शीर्ष और किनारे होते हैं जो शीर्षों को जोड़ते हैं। यह अध्याय यह नहीं मानता कि आपको ग्राफ़ सिद्धांत या पृथक गणित का कोई पूर्व ज्ञान है। हम ग्राफ़ को परिभाषित करने के लिए सादे और सरल शब्दों का उपयोग करते हैं।

ग्राफ़ क्या है? ग्राफ़ एक गणितीय संरचना है जो वास्तविक दुनिया में संस्थाओं के बीच संबंधों का प्रतिनिधित्व करता है। उदाहरण के लिए, ऊपर चित्र में ग्राफ शहरों के बीच उड़ानों का प्रतिनिधित्व करता है, और नीचे चित्र (बी) में ग्राफ भूमि द्रव्यमान के बीच पुलों का प्रतिनिधित्व करता है।

एक ग्राफ़ में शीर्षों का एक गैर-रिक्त सेट होता है (जिसे नोड्स या बिंदुओं के रूप में भी जाना जाता है), और किनारों का एक सेट होता है जो शीर्षों को जोड़ता है। सुविधा के लिए, हम एक ग्राफ़ को G = (V, E) के रूप में परिभाषित करते हैं, जहाँ V शीर्षों के एक सेट का प्रतिनिधित्व करता है और E किनारों के एक सेट का प्रतिनिधित्व करता है। उदाहरण के लिए, नीचे दिए गए चित्र में ग्राफ़ के लिए V और E इस प्रकार हैं:

वी = {"सिएटल", "सैन फ्रांसिस्को", "लॉस एंजिल्स",
"डेनवर", "कैनसस सिटी", "शिकागो", "बोस्टन", "न्यूयॉर्क",
"अटलांटा", "मियामी", "डलास", "ह्यूस्टन"};

ई = {{"सिएटल", "सैन फ्रांसिस्को"},{"सिएटल", "शिकागो"},
{"सिएटल", "डेनवर"}, {"सैन फ्रांसिस्को", "डेनवर"},
...
};

एक ग्राफ़ निर्देशित या अप्रत्यक्ष हो सकता है। निर्देशित ग्राफ़ में, प्रत्येक किनारे की एक दिशा होती है, जो इंगित करती है कि आप किनारे के माध्यम से एक शीर्ष से दूसरे तक जा सकते हैं। आप एक निर्देशित ग्राफ का उपयोग करके माता-पिता/बच्चे के संबंधों को मॉडल कर सकते हैं, जहां शीर्ष ए से बी तक का किनारा इंगित करता है कि ए, बी का माता-पिता है। नीचे दिया गया चित्र (ए) एक निर्देशित ग्राफ दिखाता है।

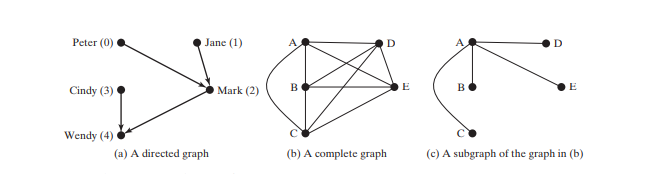
एक अप्रत्यक्ष ग्राफ़ में, आप शीर्षों के बीच दोनों दिशाओं में जा सकते हैं। नीचे दिए गए चित्र में ग्राफ अप्रत्यक्ष है।

किनारों को भारित या बिना भारित किया जा सकता है। उदाहरण के लिए, आप दो शहरों के बीच उड़ान के समय को इंगित करने के लिए ऊपर चित्र में ग्राफ़ में प्रत्येक किनारे के लिए एक वजन निर्दिष्ट कर सकते हैं।

ग्राफ़ में दो शीर्षों को आसन्न कहा जाता है यदि वे एक ही किनारे से जुड़े हों। इसी प्रकार, दो किनारों को आसन्न कहा जाता है यदि वे एक ही शीर्ष से जुड़े हों। ग्राफ़ में एक किनारा जो दो शीर्षों को जोड़ता है, उसे दोनों शीर्षों के लिए आपदा कहा जाता है। एक शीर्ष की डिग्री उस पर पड़ने वाले किनारों की संख्या है।

दो शीर्षों को पड़ोसी कहा जाता है यदि वे आसन्न हों। इसी प्रकार, दो किनारों को पड़ोसी कहा जाता है यदि वे आसन्न हों।

ए लूप एक किनारा है जो एक शीर्ष को अपने साथ जोड़ता है। यदि दो शीर्ष दो या दो से अधिक किनारों से जुड़े हुए हैं, तो इन किनारों को समानांतर किनारे कहा जाता है। एक सरल ग्राफ़ वह है जिसमें कोई लूप या समानांतर किनारे नहीं होते हैं। संपूर्ण ग्राफ़ में, शीर्षों के प्रत्येक दो जोड़े जुड़े हुए हैं, जैसा कि नीचे चित्र (बी) में दिखाया गया है।

एक ग्राफ़ जुड़ा हुआ है यदि ग्राफ़ में किन्हीं दो शीर्षों के बीच कोई पथ मौजूद है। ग्राफ़ G का एक सबग्राफ एक ग्राफ़ है जिसका शीर्ष सेट G का एक उपसमुच्चय है और जिसका किनारा सेट G का एक उपसमुच्चय है। उदाहरण के लिए, ऊपर चित्र (c) में ग्राफ़ एक है ऊपर चित्र (बी) में ग्राफ़ का उपग्राफ़।

मान लें कि ग्राफ़ जुड़ा हुआ है और अप्रत्यक्ष है। एक चक्र एक बंद पथ है जो एक शीर्ष से शुरू होता है और उसी शीर्ष पर समाप्त होता है। एक कनेक्टेड ग्राफ़ एक पेड़ है यदि इसमें चक्र नहीं हैं। ग्राफ़ G का एक फैला हुआ पेड़, G का एक जुड़ा हुआ सबग्राफ है और सबग्राफ एक ऐसा पेड़ है जिसमें G के सभी शीर्ष शामिल हैं।