यह खंड फूट डालो और जीतो का उपयोग करके बिंदुओं की निकटतम जोड़ी खोजने के लिए कुशल एल्गोरिदम प्रस्तुत करता है। बिंदुओं के एक सेट को देखते हुए, निकटतम जोड़ी की समस्या उन दो बिंदुओं को ढूंढना है जो एक-दूसरे के सबसे करीब हैं। जैसा कि नीचे चित्र में दिखाया गया है, निकटतम-जोड़ी एनीमेशन में दो निकटतम बिंदुओं को जोड़ने के लिए एक रेखा खींची गई है।

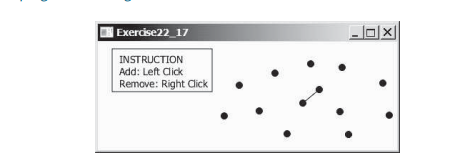
केस स्टडी: निकटतम जोड़ी ढूंढना, बिंदुओं की निकटतम जोड़ी खोजने के लिए एक क्रूर-बल एल्गोरिथ्म प्रस्तुत किया। एल्गोरिथम सभी बिंदुओं के जोड़े के बीच की दूरी की गणना करता है और न्यूनतम दूरी वाले जोड़े को ढूंढता है। स्पष्ट रूप से, एल्गोरिथ्म O(n^2) समय लेता है। क्या हम एक अधिक कुशल एल्गोरिदम डिज़ाइन कर सकते हैं?

हम इस समस्या को हल करने के लिए फूट डालो और जीतो नामक दृष्टिकोण का उपयोग करेंगे। दृष्टिकोण समस्या को उप-समस्याओं में विभाजित करता है, उप-समस्याओं को हल करता है, फिर संपूर्ण समस्या का समाधान प्राप्त करने के लिए उप-समस्याओं के समाधानों को जोड़ता है। गतिशील प्रोग्रामिंग दृष्टिकोण के विपरीत, बांटो और जीतो दृष्टिकोण में उपसमस्याएं ओवरलैप नहीं होती हैं। एक उपसमस्या छोटे आकार की मूल समस्या की तरह होती है, इसलिए आप समस्या को हल करने के लिए रिकर्सन लागू कर सकते हैं। वास्तव में, पुनरावर्ती समस्याओं के सभी समाधान फूट डालो और जीतो दृष्टिकोण का पालन करते हैं।

नीचे दिए गए चरण बताते हैं कि फूट डालो और जीतो दृष्टिकोण का उपयोग करके निकटतम जोड़ी समस्या को कैसे हल किया जाए।

• चरण 1: बिंदुओं को x-निर्देशांक के बढ़ते क्रम में क्रमबद्ध करें। समान x-निर्देशांक वाले बिंदुओं के लिए, y-निर्देशांक पर क्रमबद्ध करें। इसके परिणामस्वरूप अंकों की एक क्रमबद्ध सूची S बनती है।
• चरण 2: क्रमबद्ध सूची में मध्यबिंदु का उपयोग करके एस को समान आकार के दो उपसमूहों, एस1 और एस2 में विभाजित करें। माना मध्यबिंदु S1 में है। S1 और S2 में निकटतम जोड़ी को पुनरावर्ती रूप से खोजें। मान लीजिए कि d1 और d2 क्रमशः दो उपसमूहों में निकटतम युग्मों की दूरी को दर्शाते हैं।
• चरण 3: S1 में एक बिंदु और S2 में एक बिंदु के बीच निकटतम जोड़ी ढूंढें और उनकी दूरी को d3 के रूप में निरूपित करें। निकटतम जोड़ी वह है जिसकी दूरी न्यूनतम (d1, d2, d3) है।

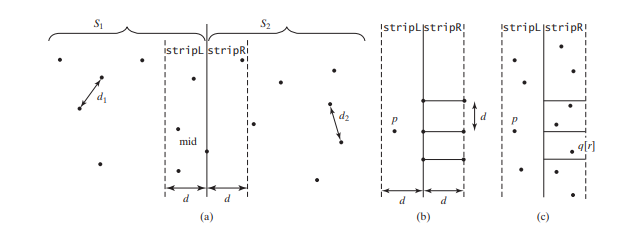
चयन क्रम में O(n^2) समय लगता है। चरण 1 O(n log n) समय में किया जा सकता है। चरण 3 O(n) समय में किया जा सकता है। मान लीजिए d = मिनट(d1, d2)। हम पहले से ही जानते हैं कि निकटतम जोड़ी की दूरी d से बड़ी नहीं हो सकती। S1 में एक बिंदु और S2 में एक बिंदु के लिए S में निकटतम जोड़ी बनाना, बायां बिंदु stripL में और दायां बिंदु stripR में होना चाहिए, जैसा कि नीचे चित्र में दिखाया गया है ( ए)।

स्ट्रिपएल में एक बिंदु पी के लिए, आपको केवल डी एक्स 2डी आयत के भीतर एक सही बिंदु पर विचार करने की आवश्यकता है, जैसा कि नीचे (बी) में दिखाया गया है। आयत के बाहर कोई भी दायाँ बिंदु p के साथ निकटतम युग्म नहीं बना सकता है। चूँकि S2 में निकटतम जोड़ी की दूरी d से अधिक या उसके बराबर है, इसलिए अधिकतम छह हो सकते हैं
आयत में बिंदु. इस प्रकार, stripL में प्रत्येक बिंदु के लिए, stripR में अधिकतम छह बिंदुओं पर विचार करने की आवश्यकता है।

stripL में प्रत्येक बिंदु p के लिए, आप stripR में संबंधित dX 2डी आयत क्षेत्र में बिंदुओं का पता कैसे लगाते हैं? यह कुशलता से किया जा सकता है यदि stripL और stripR में बिंदुओं को उनके y-निर्देशांक के बढ़ते क्रम में क्रमबद्ध किया जाए। मान लीजिए कि pointOrderedOnY y-निर्देशांक के बढ़ते क्रम में क्रमबद्ध बिंदुओं की सूची है। pointOrderedOnY एल्गोरिदम में पहले से प्राप्त किया जा सकता है। stripL और stripR को चरण 3 में pointOrderedOnY से प्राप्त किया जा सकता है जैसा कि नीचे दिए गए कोड में दिखाया गया है।

pointOrderedOnY में प्रत्येक बिंदु p के लिए
यदि (p S1 और मध्यx में है - p.x स्ट्रिपएल में पी जोड़ें;
अन्यथा यदि (p S2 और p.x में है - मध्य x स्ट्रिपआर में पी जोड़ें;

मान लीजिए कि stripL और stripR में बिंदु {p0, p1, ... , pk} और {q0, q1, ... , qt} हैं, जैसा कि इसमें दिखाया गया है ऊपर चित्र (सी)। stripL में एक बिंदु और stripR में एक बिंदु के बीच निकटतम जोड़ी नीचे दिए गए कोड में वर्णित एल्गोरिदम का उपयोग करके पाई जा सकती है।

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



stripL के बिंदुओं को इस क्रम में p0, p1, ..., pk से माना जाता है। stripL में एक बिंदु p के लिए, stripR में उन बिंदुओं को छोड़ें जो p.y – d (पंक्तियाँ 5-6) से नीचे हैं। एक बार एक बिंदु छूट जाने पर उस पर विचार नहीं किया जाएगा। जबकि लूप (लाइनें 9-17) जांचता है कि क्या (p, q[r1]) एक संभावित निकटतम जोड़ी है। अधिकतम छह ऐसे q[r1] जोड़े हैं, क्योंकि stripR में दो बिंदुओं के बीच की दूरी d से कम नहीं हो सकती। तो चरण 3 में निकटतम जोड़ी खोजने की जटिलता O(n) है।

ध्यान दें कि उपरोक्त चरणों में चरण 1 बिंदुओं को क्रमबद्ध करने के लिए केवल एक बार किया जाता है। मान लें कि सभी बिंदु क्रमबद्ध हैं। मान लीजिए T(n) इस एल्गोरिथम के लिए समय जटिलता को दर्शाता है। इस प्रकार,



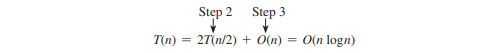
इसलिए, बिंदुओं की निकटतम जोड़ी O(n log n) समय में पाई जा सकती है।