एल्गोरिदम डिज़ाइन किसी समस्या को हल करने के लिए गणितीय प्रक्रिया विकसित करना है। एल्गोरिथम विश्लेषण एक एल्गोरिथम के प्रदर्शन की भविष्यवाणी करना है। पिछले दो अध्यायों ने क्लासिक डेटा संरचनाओं (सूचियाँ, स्टैक, कतार, प्राथमिकता कतार, सेट और मानचित्र) की शुरुआत की और समस्याओं को हल करने के लिए उन्हें लागू किया। यह अध्याय कुशल एल्गोरिदम विकसित करने के लिए सामान्य एल्गोरिदमिक तकनीकों (डायनामिक प्रोग्रामिंग, डिवाइड-एंड-कॉनकर और बैकट्रैकिंग) को पेश करने के लिए विभिन्न उदाहरणों का उपयोग करेगा।

बिग ओ नोटेशन इनपुट आकार के आधार पर एल्गोरिदम समय जटिलता को मापने के लिए एक फ़ंक्शन प्राप्त करता है। आप फ़ंक्शन में गुणक स्थिरांक और गैर-प्रभावी शब्दों को अनदेखा कर सकते हैं। मान लीजिए कि दो एल्गोरिदम एक ही कार्य करते हैं, जैसे खोज (रैखिक खोज बनाम बाइनरी खोज)। इनमें से कोनसा बेहतर है? इस प्रश्न का उत्तर देने के लिए, आप इन एल्गोरिदम को लागू कर सकते हैं और निष्पादन समय प्राप्त करने के लिए प्रोग्राम चला सकते हैं। लेकिन इस दृष्टिकोण में दो समस्याएं हैं:

• सबसे पहले, कंप्यूटर पर कई कार्य एक साथ चलते हैं। किसी विशेष प्रोग्राम का निष्पादन समय सिस्टम लोड पर निर्भर करता है।
• दूसरा, निष्पादन समय विशिष्ट इनपुट पर निर्भर करता है। उदाहरण के लिए, रैखिक खोज और बाइनरी खोज पर विचार करें। यदि खोजा जाने वाला कोई तत्व सूची में सबसे पहले होता है, तो रैखिक खोज उस तत्व को बाइनरी खोज की तुलना में जल्दी ढूंढ लेगी।

एल्गोरिदम के निष्पादन समय को मापकर उनकी तुलना करना बहुत कठिन है। इन समस्याओं को दूर करने के लिए, कंप्यूटर और विशिष्ट इनपुट से स्वतंत्र एल्गोरिदम का विश्लेषण करने के लिए एक सैद्धांतिक दृष्टिकोण विकसित किया गया था। यह दृष्टिकोण इनपुट के आकार पर परिवर्तन के प्रभाव का अनुमान लगाता है। इस तरह, आप देख सकते हैं कि इनपुट आकार बढ़ने पर एल्गोरिदम का निष्पादन समय कितनी तेजी से बढ़ता है, इसलिए आप उनकी विकास दर की जांच करके दो एल्गोरिदम की तुलना कर सकते हैं।

रैखिक खोज पर विचार करें। रैखिक खोज एल्गोरिदम कुंजी की तुलना सरणी में तत्वों के साथ क्रमिक रूप से करता है जब तक कि कुंजी नहीं मिल जाती या सरणी समाप्त नहीं हो जाती। यदि कुंजी सरणी में नहीं है, तो उसे आकार की सरणी के लिए n तुलना की आवश्यकता होती है n। यदि कुंजी सरणी में है, तो उसे औसतन n/2 तुलनाओं की आवश्यकता होती है। एल्गोरिदम का निष्पादन समय सरणी के आकार के समानुपाती होता है। यदि आप सरणी का आकार दोगुना करते हैं, तो आप तुलनाओं की संख्या दोगुनी होने की उम्मीद करेंगे। एल्गोरिथम एक रैखिक दर से बढ़ता है। विकास दर का परिमाण का क्रम n है। कंप्यूटर वैज्ञानिक "परिमाण के क्रम" को दर्शाने के लिए बिग ओ नोटेशन का उपयोग करते हैं। इस नोटेशन का उपयोग करते हुए, रैखिक खोज एल्गोरिदम की जटिलता O(n) है, जिसे "n का क्रम" के रूप में उच्चारित किया जाता है। हम O(n) की समय जटिलता वाले एक एल्गोरिदम को एक रैखिक एल्गोरिदम कहते हैं, और यह एक रैखिक विकास दर प्रदर्शित करता है।

समान इनपुट आकार के लिए, इनपुट के आधार पर एल्गोरिदम का निष्पादन समय भिन्न हो सकता है। जिस इनपुट के परिणामस्वरूप सबसे कम निष्पादन समय होता है उसे सर्वोत्तम-केस इनपुट कहा जाता है, और जिस इनपुट के परिणामस्वरूप सबसे लंबे निष्पादन समय में परिणाम होता है वह सबसे खराब-केस इनपुट होता है। सर्वोत्तम स्थिति विश्लेषण और
सबसे खराब स्थिति विश्लेषण में उनके सर्वोत्तम स्थिति वाले इनपुट और सबसे खराब स्थिति वाले इनपुट के लिए एल्गोरिदम का विश्लेषण करना शामिल है। सर्वोत्तम स्थिति और सबसे खराब स्थिति का विश्लेषण प्रतिनिधि नहीं है, लेकिन सबसे खराब स्थिति का विश्लेषण बहुत उपयोगी है। आप निश्चिंत हो सकते हैं कि एल्गोरिदम कभी भी सबसे खराब स्थिति से धीमा नहीं होगा।
एक औसत-मामला विश्लेषण एक ही आकार के सभी संभावित इनपुट के बीच समय की औसत मात्रा निर्धारित करने का प्रयास करता है। औसत-केस विश्लेषण आदर्श है, लेकिन इसे निष्पादित करना कठिन है, क्योंकि कई समस्याओं के लिए विभिन्न इनपुट उदाहरणों की सापेक्ष संभावनाओं और वितरण को निर्धारित करना कठिन है। सबसे खराब स्थिति का विश्लेषण करना आसान होता है, इसलिए विश्लेषण आम तौर पर सबसे खराब स्थिति के लिए किया जाता है।

रैखिक खोज एल्गोरिदम को सबसे खराब स्थिति में n तुलना की आवश्यकता होती है और औसत मामले में n/2 तुलना की आवश्यकता होती है यदि आप लगभग हमेशा सूची में किसी ज्ञात चीज़ की तलाश में रहते हैं। बिग ओ नोटेशन का उपयोग करते हुए, दोनों मामलों में ओ(एन) समय की आवश्यकता होती है। गुणक स्थिरांक (1/2) को छोड़ा जा सकता है। एल्गोरिथम विश्लेषण विकास दर पर केंद्रित है। गुणक स्थिरांक का विकास दर पर कोई प्रभाव नहीं पड़ता है। n/2 या 100_n_ के लिए विकास दर n के समान है, जैसा कि नीचे दी गई तालिका में दिखाया गया है, विकास दर। इसलिए, O(n) = O(n/2) = O(100n).

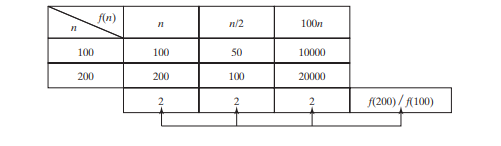
एन तत्वों की एक सरणी में अधिकतम संख्या खोजने के लिए एल्गोरिदम पर विचार करें। यदि n 2 है तो अधिकतम संख्या ज्ञात करने के लिए एक तुलना की आवश्यकता होती है; यदि n 3 है, तो दो तुलनाएँ। सामान्य तौर पर, n तत्वों की सूची में अधिकतम संख्या ज्ञात करने के लिए n - 1 तुलना की आवश्यकता होती है। एल्गोरिथम विश्लेषण बड़े इनपुट आकार के लिए है। यदि इनपुट आकार छोटा है, तो एल्गोरिदम की दक्षता का अनुमान लगाने का कोई महत्व नहीं है। जैसे-जैसे n बड़ा होता जाता है, अभिव्यक्ति n-1 में n भाग जटिलता पर हावी होता जाता है। बिग ओ नोटेशन आपको नॉनडोमिनेटिंग भाग को अनदेखा करने की अनुमति देता है (उदाहरण के लिए,
में -1 अभिव्यक्ति n - 1) और महत्वपूर्ण भाग को हाइलाइट करें (उदाहरण के लिए, अभिव्यक्ति n - 1 में n)। इसलिए, इस एल्गोरिदम की जटिलता O(n) है।

बिग ओ नोटेशन इनपुट आकार के संबंध में एल्गोरिदम के निष्पादन समय का अनुमान लगाता है। यदि समय इनपुट आकार से संबंधित नहीं है, तो एल्गोरिदम को O(1) नोटेशन के साथ निरंतर समय लेने के लिए कहा जाता है। उदाहरण के लिए, एक विधि जो किसी सरणी में दिए गए सूचकांक पर एक तत्व को पुनः प्राप्त करती है
इसमें निरंतर समय लगता है, क्योंकि सरणी का आकार बढ़ने के साथ समय नहीं बढ़ता है।

एल्गोरिदम विश्लेषण में निम्नलिखित गणितीय योग अक्सर उपयोगी होते हैं:

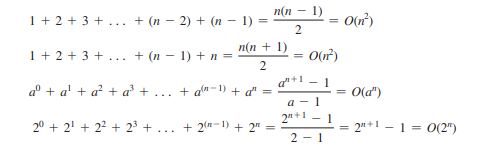
समय जटिलता बिग-ओ नोटेशन का उपयोग करके निष्पादन समय का एक माप है। इसी तरह, आप बिग-ओ नोटेशन का उपयोग करके अंतरिक्ष जटिलता को भी माप सकते हैं। अंतरिक्ष जटिलता एक एल्गोरिदम द्वारा उपयोग की जाने वाली मेमोरी स्पेस की मात्रा को मापता है। पुस्तक में प्रस्तुत अधिकांश एल्गोरिदम के लिए स्थान जटिलता O(n) है। यानी, वे इनपुट आकार में रैखिक विकास दर प्रदर्शित करते हैं। उदाहरण के लिए, रैखिक खोज के लिए स्थान जटिलता O(n) है।