ग्राफ़ की गहराई-पहली खोज ग्राफ़ में एक शीर्ष से शुरू होती है और बैकट्रैकिंग से पहले जहां तक ​​​​संभव हो ग्राफ़ में सभी शीर्षों पर जाती है।
ग्राफ़ की गहराई-पहली खोज, ट्री ट्रैवर्सल, ट्री ट्रैवर्सल में चर्चा किए गए पेड़ की गहराई-पहली खोज की तरह है। किसी पेड़ के मामले में, खोज जड़ से शुरू होती है। ग्राफ़ में, खोज किसी भी शीर्ष से शुरू हो सकती है।

किसी पेड़ की गहराई से खोज पहले जड़ तक जाती है, फिर जड़ के उपवृक्षों तक पुनरावर्ती रूप से जाती है। इसी प्रकार, ग्राफ़ की गहराई-पहली खोज पहले एक शीर्ष पर जाती है, फिर यह उस शीर्ष से सटे सभी शीर्षों पर पुनरावर्ती रूप से जाती है। अंतर यह है कि ग्राफ़ में चक्र शामिल हो सकते हैं, जिससे अनंत पुनरावृत्ति हो सकती है। इस समस्या से बचने के लिए, आपको उन चोटियों को ट्रैक करना होगा जिन पर पहले ही दौरा किया जा चुका है।

खोज को गहराई-पहले कहा जाता है क्योंकि यह ग्राफ़ में यथासंभव "गहराई" से खोज करता है। खोज किसी शीर्ष v से शुरू होती है। v पर जाने के बाद, यह v के एक अज्ञात पड़ोसी से मुलाकात करता है। यदि v का कोई अज्ञात पड़ोसी नहीं है, तो खोज उस शीर्ष पर वापस आती है जहां से यह v तक पहुंचा था। हम मानते हैं कि ग्राफ जुड़ा हुआ है और खोज शुरू हो रही है। किसी भी शीर्ष से सभी शीर्षों तक पहुंचा जा सकता है।

गहराई-प्रथम खोज एल्गोरिथम

गहराई-पहली खोज के लिए एल्गोरिदम नीचे दिए गए कोड में वर्णित है।

इनपुट: जी = (वी, ई) और एक प्रारंभिक शीर्ष वी
आउटपुट: एक DFS पेड़ जिसकी जड़ें v
पर हैं 1 ट्री डीएफएस(वर्टेक्स वी) {
2 विज़िट वी;
वी के प्रत्येक पड़ोसी के लिए 3
4 यदि (डब्ल्यू का दौरा नहीं किया गया है) {
5 पेड़ में w के लिए मूल के रूप में v सेट करें;
6 डीएफएस(डब्ल्यू);
7 }
8 }

आप यह दर्शाने के लिए कि किसी शीर्ष पर विज़िट किया गया है या नहीं, isVisited नामक सरणी का उपयोग कर सकते हैं। प्रारंभ में, isVisited[i] प्रत्येक शीर्ष i के लिए false है। एक बार जब किसी शीर्ष, मान लीजिए v, का दौरा किया जाता है, तो isVisited[v] को true पर सेट कर दिया जाता है।

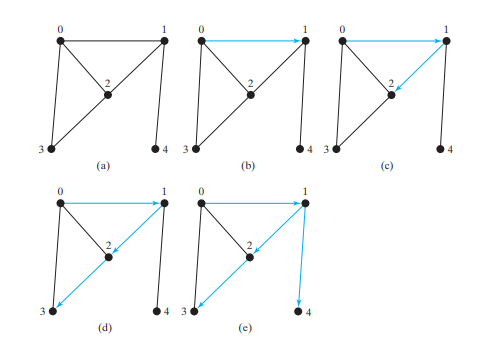
नीचे चित्र (ए) में ग्राफ़ पर विचार करें। मान लीजिए कि हम शीर्ष 0 से गहराई-पहली खोज शुरू करते हैं। पहले 0 पर जाएँ, फिर उसके किसी पड़ोसी, मान लीजिए 1 पर जाएँ। अब 1 पर जाएँ, जैसा कि नीचे चित्र (बी) में दिखाया गया है। वर्टेक्स 1 के तीन पड़ोसी हैं- 0, 2, और 4. चूँकि 0 का दौरा पहले ही किया जा चुका है, आप या तो 2 या 4 का दौरा करेंगे। आइए 2 चुनें। अब 2 का दौरा किया गया है, जैसा कि नीचे चित्र (सी) में दिखाया गया है। वर्टेक्स 2 के तीन पड़ोसी हैं: 0, 1, और 3. चूँकि 0 और 1 पहले ही देखे जा चुके हैं, इसलिए 3 चुनें। 3 अब देखा जा चुका है, जैसा कि नीचे चित्र (डी) में दिखाया गया है। इस बिंदु पर, शीर्षों का दौरा इस क्रम में किया गया है:

0, 1, 2, 3

चूंकि 3 के सभी पड़ोसियों का दौरा किया जा चुका है, इसलिए 2 पर वापस जाएं। चूंकि 2 के सभी शीर्षों का दौरा किया जा चुका है, इसलिए 1 पर वापस जाएं। 4, 1 के निकट है, लेकिन 4 पर नहीं गया है। इसलिए, 4 पर जाएँ, जैसा कि नीचे चित्र (ई) में दिखाया गया है। चूँकि 4 के सभी पड़ोसियों का दौरा किया जा चुका है, 1 पर वापस जाएँ।
चूँकि 1 के सभी पड़ोसियों का दौरा किया जा चुका है, इसलिए 0 पर वापस जाएँ। चूँकि 0 के सभी पड़ोसियों का दौरा किया जा चुका है, इसलिए खोज समाप्त होती है।

चूंकि प्रत्येक किनारे और प्रत्येक शीर्ष पर केवल एक बार दौरा किया जाता है, dfs विधि की समय जटिलता O(|E| |V|) है, जहां |E | किनारों की संख्या और |V| शीर्षों की संख्या को दर्शाता है।

गहराई-प्रथम खोज का कार्यान्वयन

उपरोक्त कोड में डीएफएस के लिए एल्गोरिदम रिकर्सन का उपयोग करता है। इसे लागू करने के लिए रिकर्सन का उपयोग करना स्वाभाविक है। वैकल्पिक रूप से, आप स्टैक का उपयोग कर सकते हैं।

dfs(int v) विधि AbstractGraph.java में पंक्ति 164-193 में लागू की गई है। यह मूल के रूप में शीर्ष v के साथ Tree वर्ग का एक उदाहरण देता है। विधि सूची में खोजे गए शीर्षों को संग्रहीत करती है searchOrder (पंक्ति 165), सरणी में प्रत्येक शीर्ष के मूल को parent (पंक्ति 166), और isVisited सरणी यह ​​इंगित करने के लिए कि क्या किसी शीर्ष का दौरा किया गया है (पंक्ति 171)। यह गहराई से पहली खोज (पंक्ति 174) करने के लिए सहायक विधि dfs(v,parent, searchOrder, isVisited) का आह्वान करता है।

पुनरावर्ती सहायक विधि में, खोज शीर्ष u से शुरू होती है। u को लाइन 184 में searchOrder में जोड़ा गया है और विज़िट (लाइन 185) के रूप में चिह्नित किया गया है। u के प्रत्येक न देखे गए पड़ोसी के लिए, गहन-पहली खोज करने के लिए विधि को पुनरावर्ती रूप से लागू किया जाता है। जब एक शीर्ष e.v का दौरा किया जाता है, तो e.v का पैरेंट parent[e.v] (पंक्ति 189) में संग्रहीत किया जाता है। विधि तब वापस आती है जब किसी कनेक्टेड ग्राफ़ के लिए, या किसी कनेक्टेड घटक में सभी शीर्षों का दौरा किया जाता है।

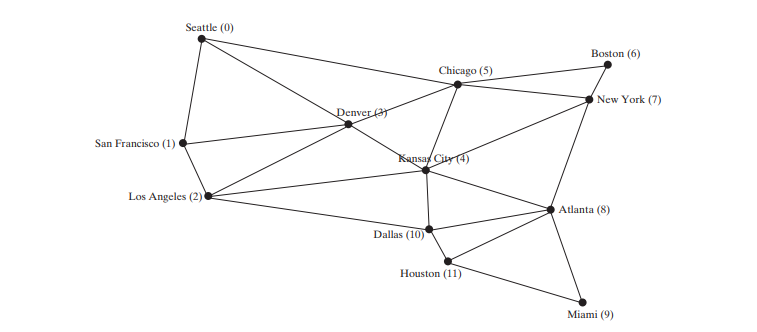
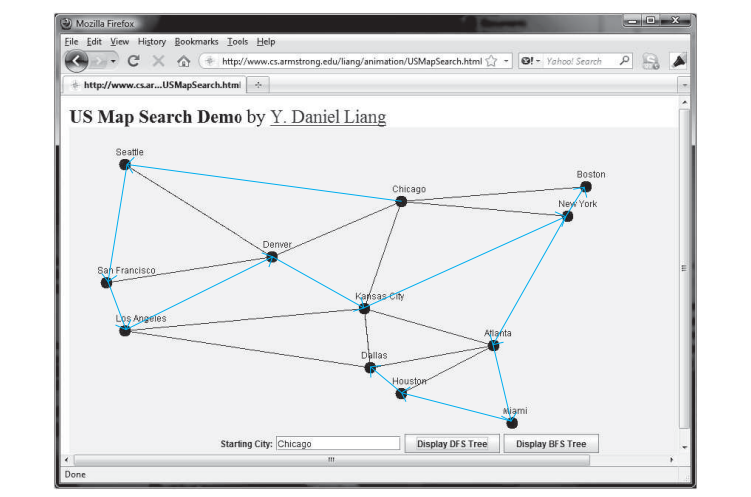
नीचे दिया गया कोड एक परीक्षण कार्यक्रम देता है जो शिकागो से शुरू होने वाले चित्र में ऊपर दिए गए ग्राफ़ के लिए एक डीएफएस प्रदर्शित करता है। शिकागो से शुरू होने वाले डीएफएस का चित्रमय चित्रण नीचे चित्र में दिखाया गया है।

public class TestDFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph graph = new UnweightedGraph(vertices, edges);
        AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago"));

        java.util.List searchOrders = dfs.getSearchOrder();
        System.out.println(dfs.getNumberOfVerticesFound()   " vertices are searched in this DFS order:");
        for(int i = 0; i 



इस डीएफएस क्रम में 12 शीर्ष खोजे गए हैं:

 शिकागो सिएटल सैन फ्रांसिस्को लॉस एंजिल्स डेनवर

 कैनसस सिटी न्यूयॉर्क बोस्टन अटलांटा मियामी ह्यूस्टन डलास

सिएटल का जनक शिकागो है

सैन फ्रांसिस्को का जनक सिएटल है

लॉस एंजिल्स का जनक सैन फ्रांसिस्को है

डेनवर का मूल निवासी लॉस एंजिल्स है

कैनसस सिटी का जनक डेनवर है

बोस्टन का जनक न्यूयॉर्क है

न्यूयॉर्क का जनक कैनसस सिटी है

अटलांटा का जनक न्यूयॉर्क है

मियामी का जनक अटलांटा है

डलास के माता-पिता ह्यूस्टन हैं

ह्यूस्टन का जनक मियामी है




  
  
  डीएफएस के अनुप्रयोग


गहराई-पहली खोज का उपयोग कई समस्याओं को हल करने के लिए किया जा सकता है, जैसे कि निम्नलिखित:

यह पता लगाना कि कोई ग्राफ़ कनेक्ट है या नहीं। किसी भी शीर्ष से शुरू करके ग्राफ़ खोजें। यदि खोजे गए शीर्षों की संख्या ग्राफ़ में शीर्षों की संख्या के समान है, तो ग्राफ़ जुड़ा हुआ है। अन्यथा, ग्राफ़ कनेक्ट नहीं है।
यह पता लगाना कि क्या दो शीर्षों के बीच कोई पथ है।
दो शीर्षों के बीच पथ ढूँढना।
सभी जुड़े हुए घटकों को ढूँढना। एक कनेक्टेड घटक एक अधिकतम कनेक्टेड सबग्राफ है जिसमें प्रत्येक जोड़ी कोने एक पथ से जुड़े होते हैं।
यह पता लगाना कि ग्राफ़ में कोई चक्र है या नहीं।
ग्राफ़ में एक चक्र ढूँढना।
हैमिल्टनियन पथ/चक्र ढूँढना। ग्राफ़ में एक हैमिल्टनियन पथ एक ऐसा पथ है जो ग्राफ़ में प्रत्येक शीर्ष पर ठीक एक बार जाता है। एक हैमिल्टनियन चक्र ग्राफ़ में प्रत्येक शीर्ष पर ठीक एक बार जाता है और प्रारंभिक शीर्ष पर लौट आता है।
AbstractGraph.java में dfs विधि का उपयोग करके पहली छह समस्याओं को आसानी से हल किया जा सकता है। हैमिल्टनियन पथ/चक्र को खोजने के लिए, आपको सबसे लंबे पथ की ओर ले जाने वाले पथ को खोजने के लिए सभी संभावित डीएफएस का पता लगाना होगा। हैमिल्टनियन पथ/चक्र के कई अनुप्रयोग हैं, जिनमें सुप्रसिद्ध नाइट्स टूर समस्या का समाधान भी शामिल है।