क्या आपने कभी सोचा है कि कैसीनो हमेशा जीतते हुए क्यों दिखते हैं? "बीटिंग द ऑड्स: द मैथमेटिक्स बिहाइंड द कैसिनो प्रॉफिट्स" में, हम सरल गणित और चतुर रणनीतियों का पता लगाएंगे जो सुनिश्चित करते हैं कि कैसीनो लंबे समय में पैसा कमाते हैं। समझने में आसान उदाहरणों और मोंटे कार्लो सिमुलेशन के माध्यम से, हम घर के किनारे के पीछे के रहस्यों को उजागर करेंगे। यह जानने के लिए तैयार हो जाइए कि कैसे कैसिनो परिस्थितियों को अपने पक्ष में कर लेते हैं!

हाउस एज को समझना

कैसीनो की दुनिया में हाउस एज एक मौलिक अवधारणा है। यह उस औसत लाभ का प्रतिनिधित्व करता है जो कैसीनो खिलाड़ियों द्वारा लगाए गए प्रत्येक दांव से प्राप्त करने की उम्मीद करता है। अनिवार्य रूप से, यह प्रत्येक दांव का प्रतिशत है जिसे कैसीनो लंबे समय तक बरकरार रखेगा।

हाउस एज मौजूद है क्योंकि कैसीनो खेल की "सही संभावनाओं" के अनुसार जीतने वाले दांव का भुगतान नहीं करते हैं। सच्ची संभावनाएँ किसी घटना के घटित होने की वास्तविक संभावना को दर्शाती हैं। थोड़े कम अंतर पर भुगतान करके, कैसीनो यह सुनिश्चित करते हैं कि वे समय के साथ लाभ कमाएँ।

हाउस एज (एचई) को खिलाड़ी के मूल दांव के प्रतिशत के रूप में व्यक्त कैसीनो लाभ के रूप में परिभाषित किया गया है।

** यूरोपीय रूलेट ** में केवल एक हरा शून्य है, जो इसे कुल 37 संख्याएँ देता है। यदि कोई खिलाड़ी रेड पर $1 का दांव लगाता है, तो उसके पास $1 जीतने का 18/37 मौका है और $1 खोने का 19/37 मौका है। अपेक्षित मान है:

अपेक्षित मूल्य=( 1 × 18/37 ​) ( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≈ −2.7%

इसलिए, यूरोपीय रूलेट में हाउस एज (एचई) लगभग 2.7% है।

आइए इसे और अधिक समझने के लिए अपना खुद का गेम बनाएं, एक सरल पासा रोल गेम।

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll 

इस गेम में:

• यदि रोल 100 है तो खिलाड़ी के पास हारने की 1/100 संभावना है।

• यदि रोल 1 और 50 के बीच है तो खिलाड़ी के पास हारने की 50/100 संभावना है।

• यदि रोल 51 और 99 के बीच है तो खिलाड़ी के जीतने की 49/100 संभावना है।

अपेक्षित मान =(1× 49/100​) ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100 ​ ≈ −2%

इसलिए, घर का किनारा 2% है।

मोंटे कार्लो सिमुलेशन को समझना

मोंटे कार्लो सिमुलेशन एक शक्तिशाली उपकरण है जिसका उपयोग किसी प्रक्रिया के कई सिमुलेशन चलाकर और परिणामों का अवलोकन करके जटिल प्रणालियों को समझने और भविष्यवाणी करने के लिए किया जाता है। कैसीनो के संदर्भ में, मोंटे कार्लो सिमुलेशन यह दिखाने के लिए विभिन्न सट्टेबाजी परिदृश्यों का मॉडल बना सकता है कि हाउस एज दीर्घकालिक लाभप्रदता कैसे सुनिश्चित करता है। आइए जानें कि मोंटे कार्लो सिमुलेशन कैसे काम करते हैं और उन्हें एक साधारण कैसीनो गेम में कैसे लागू किया जा सकता है।

मोंटे कार्लो सिमुलेशन क्या है?

मोंटे कार्लो सिमुलेशन में एक प्रक्रिया को कई बार अनुकरण करने और परिणामों का विश्लेषण करने के लिए यादृच्छिक चर उत्पन्न करना शामिल है। हजारों या लाखों पुनरावृत्तियों को निष्पादित करके, हम संभावित परिणामों का वितरण प्राप्त कर सकते हैं और विभिन्न घटनाओं की संभावना में अंतर्दृष्टि प्राप्त कर सकते हैं।

डाइस रोल गेम में मोंटे कार्लो सिमुलेशन लागू करना

जिस पासा रोल गेम की हमने पहले चर्चा की थी, उसे मॉडल करने के लिए हम मोंटे कार्लो सिमुलेशन का उपयोग करेंगे। इससे हमें यह समझने में मदद मिलेगी कि घरेलू बढ़त समय के साथ खेल की लाभप्रदता को कैसे प्रभावित करती है।

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins  = 1
        else:
            losses  = 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

परिणामों की व्याख्या करना

इस सिमुलेशन में, हम जीत और हार के प्रतिशत का निरीक्षण करने के लिए पासा रोल गेम को 10,000,000 बार चलाते हैं। पहले से गणना की गई घरेलू बढ़त (2%) को देखते हुए, हमें उम्मीद है कि हार का प्रतिशत जीत के प्रतिशत से थोड़ा अधिक होगा।

सिमुलेशन चलाने के बाद, आपको ऐसे परिणाम दिखाई दे सकते हैं:

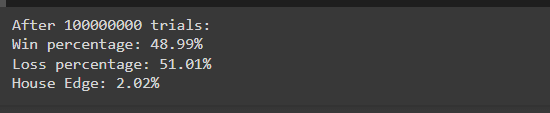
ये परिणाम सैद्धांतिक संभावनाओं (49% जीत, 51% हानि) के साथ निकटता से मेल खाते हैं, यह दर्शाता है कि बड़ी संख्या में परीक्षणों में घरेलू बढ़त कैसे प्रकट होती है। थोड़ा सा असंतुलन लंबे समय में कैसीनो की लाभप्रदता सुनिश्चित करता है।

अल्पकालिक जीत और दीर्घकालिक नुकसान की कल्पना करना

मोंटे कार्लो सिमुलेशन बार-बार यादृच्छिक नमूने के माध्यम से मॉडलिंग और परिणामों की भविष्यवाणी करने के लिए शक्तिशाली हैं। जुए के संदर्भ में, हम विभिन्न सट्टेबाजी रणनीतियों के संभावित परिणामों को समझने के लिए मोंटे कार्लो सिमुलेशन का उपयोग कर सकते हैं।

हम एक एकल दांव लगाने वाले का अनुकरण करेंगे जो प्रत्येक दौर में समान प्रारंभिक दांव लगाता है और देखेगा कि दांव की एक निर्दिष्ट संख्या पर उनके खाते का मूल्य कैसे विकसित होता है।

यहां बताया गया है कि हम मैटप्लोटलिब का उपयोग करके सट्टेबाजी यात्रा का अनुकरण और कल्पना कैसे कर सकते हैं:

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager 



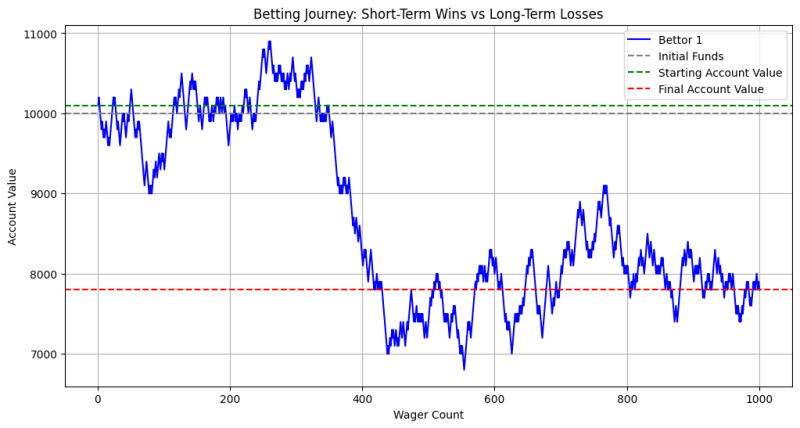
यह ग्राफ़ दिखाता है कि जीत और हार के कारण समय के साथ सट्टेबाज के खाते के मूल्य में कैसे उतार-चढ़ाव हो सकता है। प्रारंभ में, जीतने की अवधि हो सकती है (शुरुआती मूल्य के ऊपर हरी रेखा), लेकिन जैसे-जैसे दांव की संख्या बढ़ती है, हाउस एज का संचयी प्रभाव स्पष्ट हो जाता है। अंततः, सट्टेबाज के खाते का मूल्य प्रारंभिक निधि (ग्रे लाइन) की ओर या उससे नीचे गिर जाता है, जो दीर्घकालिक नुकसान का संकेत देता है।


  
  
  निष्कर्ष


कैसीनो के मुनाफे के पीछे के गणित को समझने से हाउस एज की अवधारणा के माध्यम से हर गेम में हाउस के लिए एक स्पष्ट लाभ का पता चलता है। कभी-कभार जीत के बावजूद, कैसीनो गेम में बनी संभावना यह सुनिश्चित करती है कि अधिकांश खिलाड़ी समय के साथ पैसा खो देंगे। मोंटे कार्लो सिमुलेशन इन गतिशीलता को स्पष्ट रूप से चित्रित करते हैं, यह दिखाते हुए कि कैसे अल्पकालिक जीत भी कैसीनो के सांख्यिकीय लाभ के कारण दीर्घकालिक नुकसान को छुपा सकती है। कैसीनो लाभप्रदता की गणितीय निश्चितता में यह अंतर्दृष्टि सूचित निर्णय लेने और जिम्मेदार जुआ प्रथाओं के महत्व को रेखांकित करती है।

इसके बाद, हम अतिरिक्त विज़ुअलाइज़ेशन या विविधताओं का पता लगा सकते हैं, जैसे कि विभिन्न सट्टेबाजी रणनीतियों की तुलना करना या सट्टेबाज के परिणामों पर अलग-अलग प्रारंभिक दांव के प्रभाव का विश्लेषण करना।

जुड़े रहो:

• गिटहब: ezhillragesh

• ट्विटर: ezhillragesh

• वेबसाइट: ragesh.me

अपने विचार साझा करने, प्रश्न पूछने और चर्चा में योगदान करने में संकोच न करें।

हैप्पी कोडिंग!