Le problème pondéré à neuf queues peut être réduit au problème pondéré du chemin le plus court.
La section a présenté le problème à neuf queues et l'a résolu en utilisant l'algorithme BFS. Cette section présente une variante du problème et le résout à l'aide de l'algorithme du chemin le plus court.

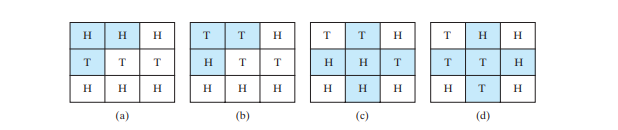
Le problème à neuf queues est de trouver le nombre minimum de mouvements qui mènent à toutes les pièces face vers le bas. Chaque mouvement lance une pièce de monnaie et ses voisines. Le problème pondéré à neuf queues attribue le nombre de retournements comme poids à chaque mouvement. Par exemple, vous pouvez remplacer les pièces de la figure ci-dessous a par celles de la figure ci-dessous b en retournant la première pièce de la première rangée et ses deux voisines. Ainsi, le poids de ce mouvement est de 3. Vous pouvez changer les pièces de la figure ci-dessous c en figure ci-dessous d en retournant la pièce centrale et ses quatre voisines. Le poids de ce mouvement est donc de 5.

Le problème pondéré à neuf queues peut être réduit à trouver le chemin le plus court entre un nœud de départ et le nœud cible dans un graphe pondéré par les bords. Le graphe comporte 512 nœuds. Créez une arête du nœud v à u s'il y a un déplacement du nœud u au nœud v. Attribuez le nombre de retournements au poids du bord.

Rappelons que dans la section, nous avons défini une classe NineTailModel pour modéliser le problème à neuf queues. Nous définissons maintenant une nouvelle classe nommée WeightedNineTailModel qui étend NineTailModel, comme le montre la figure ci-dessous.

La classe NineTailModel crée un Graph et obtient un Arbre enraciné au nœud cible 511. WeightedNineTailModel est identique à NineTailModel, sauf qu'il crée un WeightedGraph et obtient un ShortestPathTree enraciné au niveau du nœud cible 511. WeightedNineTailModel étend NineTailModel. La méthode getEdges() trouve toutes les arêtes du graphique. La méthode getNumberOfFlips(int u, int v) renvoie le nombre de retournements du nœud u au nœud v. La méthode getNumberOfFlips(int u) renvoie le nombre de retournements du nœud u au nœud cible.

Le code ci-dessous implémente WeightedNineTailModel.

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}

WeightedNineTailModel étend NineTailModel pour créer un WeightedGraph pour modéliser le problème pondéré à neuf queues (lignes 10 à 11). Pour chaque nœud u, la méthode getEdges() trouve un nœud inversé v et attribue le nombre de retournements comme poids pour le bord (v, u) (ligne 30). La méthode getNumberOfFlips(int u, int v) renvoie le nombre de retournements du nœud u au nœud v (lignes 38 à 47). Le nombre de retournements est le nombre de cellules différentes entre les
deux nœuds (ligne 44).

Le WeightedNineTailModel obtient un ShortestPathTree enraciné au nœud cible 511 (ligne 14). Notez que tree est un champ de données protégé défini dans NineTailModel et ShortestPathTree est une sous-classe de Tree. Les méthodes définies dans NineTailModel utilisent la propriété tree.

La méthode getNumberOfFlips(int u) (lignes 49 à 52) renvoie le nombre de retournements du nœud u au nœud cible, qui est le coût du chemin depuis le nœud u vers le nœud cible. Ce coût peut être obtenu en appelant la méthode getCost(u) définie dans la classe ShortestPathTree (ligne 51).

Le code ci-dessous donne un programme qui invite l'utilisateur à entrer un nœud initial et affiche le nombre minimum de retournements pour atteindre le nœud cible.

package demo;

import java.util.Scanner;

public class WeightedNineTail {

    public static void main(String[] args) {
        // Prompt the user to enter nine coins' Hs and Ts
        System.out.print("Enter the initial nine coins Hs and Ts: ");
        Scanner input = new Scanner(System.in);
        String s = input.nextLine();
        char[] initialNode = s.toCharArray();

        WeightedNineTailModel model = new WeightedNineTailModel();
        java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode));

        System.out.println("The steps to flip the coins are ");
        for (int i = 0; i 



Entrez neuf pièces initiales Hs et Ts : HHHTTTHHH

Les étapes pour lancer les pièces sont

HHH

TTT

HHH

HHH

THT

TTT

TTT

TTT

TTT

Le nombre de retournements est de 8

Le programme invite l'utilisateur à saisir un nœud initial avec neuf lettres avec une combinaison de Hs et Ts sous forme de chaîne à la ligne 8, obtient un tableau de caractères de la chaîne (ligne 9), crée un modèle (ligne 11), obtient le chemin le plus court du nœud initial au nœud cible (lignes 12-13), affiche les nœuds du chemin (lignes 16-17), et invoque getNumberOfFlips pour obtenir le nombre de retournements nécessaires pour atteindre le nœud cible (ligne 20).