Régression des k-voisins les plus proches

k-Nearest Neighbours (k-NN) est une méthode non paramétrique qui prédit la valeur de sortie en fonction de la moyenne (ou moyenne pondérée) des k points de données d'entraînement les plus proches dans l'espace des fonctionnalités. Cette approche peut modéliser efficacement des relations complexes dans les données sans assumer une forme fonctionnelle spécifique.

La méthode de régression k-NN peut être résumée comme suit :

1. Metrique de distance : l'algorithme utilise une métrique de distance (généralement la distance euclidienne) pour déterminer la « proximité » des points de données.
2. k Voisins : le paramètre k spécifie le nombre de voisins les plus proches à prendre en compte lors de la réalisation de prédictions.
3. Prédiction : la valeur prédite pour un nouveau point de données est la moyenne des valeurs de ses k voisins les plus proches.

Concepts clés

1. Non paramétrique : contrairement aux modèles paramétriques, k-NN ne prend pas de forme spécifique pour la relation sous-jacente entre les caractéristiques d'entrée et la variable cible. Cela le rend flexible dans la capture de modèles complexes.

2. Calcul de distance : le choix de la métrique de distance peut affecter considérablement les performances du modèle. Les mesures courantes incluent les distances euclidiennes, Manhattan et Minkowski.

3. Choix de k : le nombre de voisins (k) peut être choisi en fonction d'une validation croisée. Un petit k peut conduire à un surajustement, tandis qu'un grand k peut trop lisser la prédiction, voire un sous-ajustement.

Exemple de régression des k-voisins les plus proches

Cet exemple montre comment utiliser la régression k-NN avec des caractéristiques polynomiales pour modéliser des relations complexes tout en tirant parti de la nature non paramétrique de k-NN.

Exemple de code Python

1. Importer des bibliothèques

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score

Ce bloc importe les bibliothèques nécessaires à la manipulation des données, au traçage et à l'apprentissage automatique.

2. Générer des exemples de données

np.random.seed(42)  # For reproducibility
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 3 * X.ravel()   np.sin(2 * X.ravel()) * 5   np.random.normal(0, 1, 100)

Ce bloc génère des exemples de données représentant une relation avec certains bruits, simulant les variations des données du monde réel.

3. Diviser l'ensemble de données

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Ce bloc divise l'ensemble de données en ensembles de formation et de test pour l'évaluation du modèle.

4. Créer des entités polynomiales

degree = 3  # Change this value for different polynomial degrees
poly = PolynomialFeatures(degree=degree)
X_poly_train = poly.fit_transform(X_train)
X_poly_test = poly.transform(X_test)

Ce bloc génère des caractéristiques polynomiales à partir des ensembles de données de formation et de test, permettant au modèle de capturer des relations non linéaires.

5. Créer et entraîner le modèle de régression k-NN

k = 5  # Number of neighbors
knn_model = KNeighborsRegressor(n_neighbors=k)
knn_model.fit(X_poly_train, y_train)

Ce bloc initialise le modèle de régression k-NN et l'entraîne à l'aide des caractéristiques polynomiales dérivées de l'ensemble de données d'entraînement.

6. Faire des prédictions

y_pred = knn_model.predict(X_poly_test)

Ce bloc utilise le modèle entraîné pour faire des prédictions sur l'ensemble de test.

7. Tracer les résultats

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()

Ce bloc crée un nuage de points des points de données réels par rapport aux valeurs prédites du modèle de régression k-NN, visualisant la courbe ajustée.

Sortie avec k = 1 :

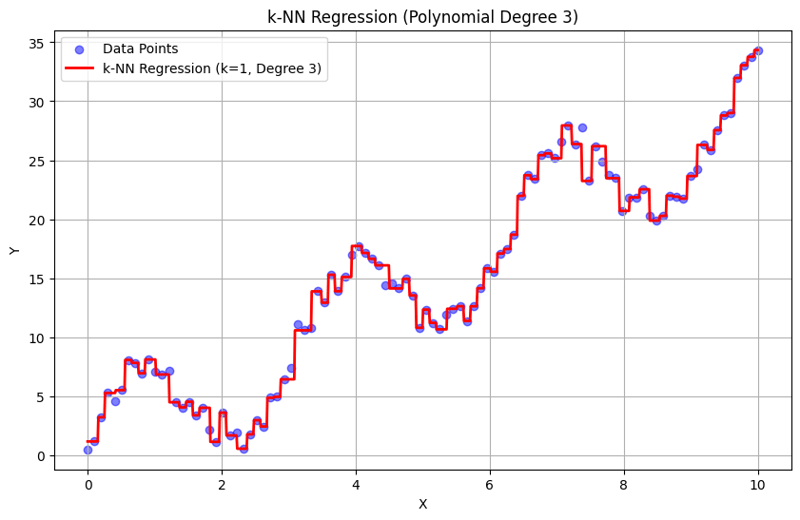
Sortie avec k = 10 :

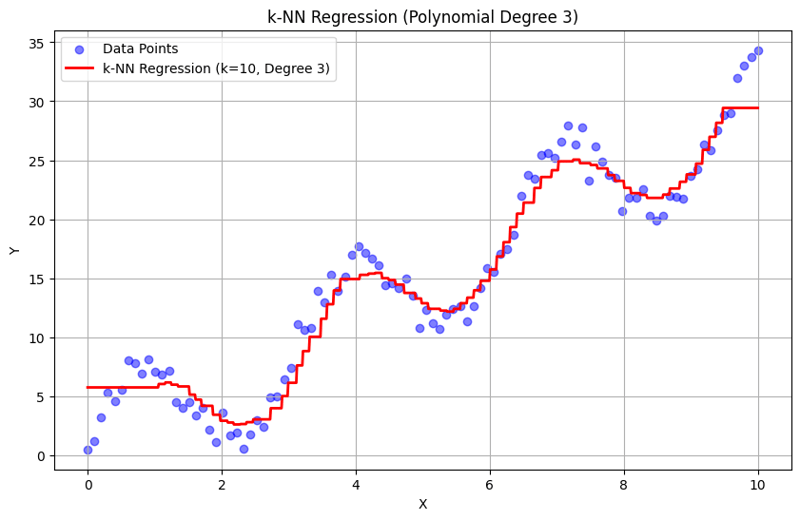
Cette approche structurée montre comment implémenter et évaluer la régression des k-plus proches voisins avec des caractéristiques polynomiales. En capturant des modèles locaux en faisant la moyenne des réponses des voisins proches, la régression k-NN modélise efficacement les relations complexes dans les données tout en fournissant une mise en œuvre simple. Le choix du k et du degré polynomial influence considérablement les performances et la flexibilité du modèle dans la capture des tendances sous-jacentes.