Le problème du sous-tableau maximum et son historique

À la fin des années 1970, le mathématicien suédois Ulf Grenander discutait d'un problème : comment analyser un tableau 2D de données d'image plus efficacement que la force brute ? Les ordinateurs étaient alors lents et les images étaient volumineuses par rapport à la RAM. Pour aggraver les choses, dans le pire des cas, la force brute prenait un temps O (n ^ 6) (complexité temporelle sextique).

Tout d'abord, Grenandier a simplifié la question : étant donné un tableau de nombres unidimensionnel, comment trouveriez-vous le plus efficacement le sous-tableau contigu avec la plus grande somme ?

Brute Force : une approche naïve avec une complexité temporelle cubique

Force brute, il faudrait deux fois moins de temps pour analyser un tableau 1D qu'un tableau 2D, donc O(n^3) pour examiner toutes les combinaisons possibles (complexité temporelle cubique).

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

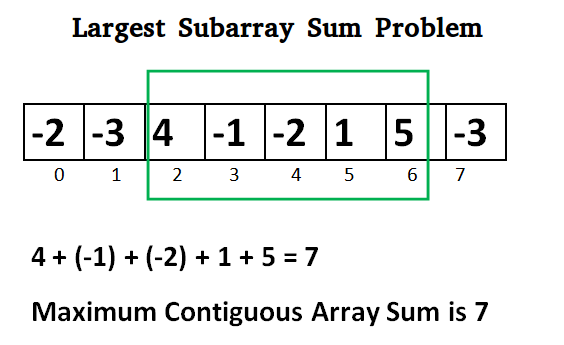
print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Optimisation O(n²) de Grenander : un pas en avant

Grenander l'a amélioré en solution O(n^2). Je n'ai pas pu trouver son code dans mes recherches, mais je suppose qu'il s'est simplement débarrassé de la boucle la plus interne qui additionne tous les nombres entre les deux indices. Au lieu de cela, nous pouvons conserver une somme cumulée tout en itérant sur le sous-tableau, réduisant ainsi le nombre de boucles de trois à deux.

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

Diviser pour mieux régner de Shamos : diviser le problème en O(n log n)

Grenander a montré le problème à l'informaticien Michael Shamos. Shamos y a réfléchi pendant une nuit et a proposé une méthode diviser pour mieux régner qui est O(n log n).

C'est assez intelligent. L'idée est de diviser le tableau en deux moitiés, puis de trouver de manière récursive la somme maximale des sous-tableaux pour chaque moitié ainsi que le sous-tableau traversant le point médian.

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

Cela réduit la complexité temporelle au temps O(nlogn) car d'abord le tableau est divisé en deux moitiés (O(logn)), puis trouver le sous-tableau de croisement maximum prend O(n)

L'algorithme de Kadane : la solution élégante O(n)

Le stasticien Jay Kadane a examiné le code et a immédiatement identifié que la solution de Shamos n'utilisait pas la contrainte de contiguïté dans le cadre de la solution.

Voici ce qu'il a réalisé

-Si un tableau ne contient que des nombres négatifs, la réponse sera toujours le plus grand nombre du tableau, en supposant que nous n'autorisons pas les sous-tableaux vides.

-Si un tableau ne contient que des nombres positifs, la réponse sera toujours d'additionner l'ensemble du tableau.

-Si vous disposez d'un tableau de nombres positifs et négatifs, vous pouvez parcourir le tableau étape par étape. Si à un moment donné le nombre que vous regardez est supérieur à la somme de tous les nombres qui l’ont précédé, la solution ne peut inclure aucun des nombres précédents. Ainsi, vous démarrez une nouvelle somme à partir du numéro actuel, tout en gardant une trace de la somme maximale rencontrée jusqu'à présent.

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

Ce que j'aime dans cet algorithme, c'est qu'il peut être appliqué à de nombreux autres problèmes. Essayez de l'adapter pour résoudre ces problèmes LeetCode :

Uns et zéros
Sous-tableau circulaire à somme maximale
Somme du sous-tableau de taille minimale
Somme maximale croissante du sous-tableau
Sous-tableau de produits maximum
Somme de sous-tableau continue
Sous-tableau à somme alternée maximale (premium)
Somme maximale du rectangle ne dépassant pas K