Énoncé du problème 1071. Le plus grand diviseur commun de chaînes

Pour deux chaînes s et t, nous disons "t divise s" si et seulement si s = t t t ... t t (c'est-à-dire que t est concaténé avec lui-même une ou plusieurs fois).

Étant donné deux chaînes str1 et str2, renvoie la plus grande chaîne x telle que x divise à la fois str1 et str2.

Mon processus de pensée

Même si le leetcode l'a marqué comme un problème facile, je dois admettre que j'ai eu du mal à trouver immédiatement une solution.

Permettez-moi de passer en revue les cas de test fournis par leetcode et de les passer en revue pour expliquer ma confusion.

Cas de test

Entrée : str1 = "ABCABC", str2 = "ABC"
Sortie : "ABC"

Entrée : str1 = "ABABAB", str2 = "ABAB"
Sortie : "AB"

À partir de l'énoncé du problème et du scénario de test 1, j'ai déterminé que nous devions générer la plus grande chaîne ("ABC") en concaténant laquelle nous pouvons obtenir les deux chaînes. (chaîne par défaut "ABC" === str2 et "ABC" "ABC" === str1).

Cependant, en regardant le cas de test 2, j'ai rapidement réalisé que ma compréhension n'était pas correcte car je devrais afficher "ABAB" car c'est la chaîne la plus longue à l'aide de laquelle je peux créer les deux chaînes. Mais je suis passé au code et j'ai commencé à élaborer une solution. (Erreur de débutant ?)

Ce qui a échoué/réussi

Je n'ai pu trouver une solution que là où :

1. trouver le PGCD de deux chaînes.
2. itérer de la longueur de la plus petite chaîne à GCD
3. prend une sous-chaîne de la plus petite chaîne à la valeur d'itération actuelle.
4. si les deux chaînes contiennent cette sous-chaîne, renvoie cette sous-chaîne comme réponse.
5. si aucune chaîne n'est trouvée, retournez "".

Comme vous pouvez le voir, ma solution a échoué pour les chaînes où str1 contient str2 mais contient également d'autres caractères supplémentaires. violant l'exigence selon laquelle s = t t ... t t.

J'ai dû me tourner vers la solution de neetcode pour obtenir de l'aide. J'ai vite compris mes problématiques :

1. Je trouvais le GCD de la longueur de la chaîne, PAS la chaîne elle-même. J'ai besoin de trouver une chaîne où, en répétant ces chaînes, je peux créer les deux chaînes sans aucun caractère restant.

2. J'ai compris pourquoi "ABAB" ne peut pas être la réponse au scénario de test 2 :

• nous devons trouver x tel qu'il divise les deux chaînes de manière égale. donc en prenant "ABAB" comme chaîne, vous pouvez créer complètement str2 mais pour str1 vous vous retrouvez avec "ABABABAB". Vous vous retrouvez avec 2 "AB" en excès et ne pouvez pas dire que vous avez créé str1 complètement en combinant x.

• "ABAB" longueur 4 et "ABABAB" longueur 6. Le GCD des 2 chaînes = 2. Par conséquent, la sortie doit être une chaîne de longueur 2.

Sortir

Complexité temporelle et spatiale

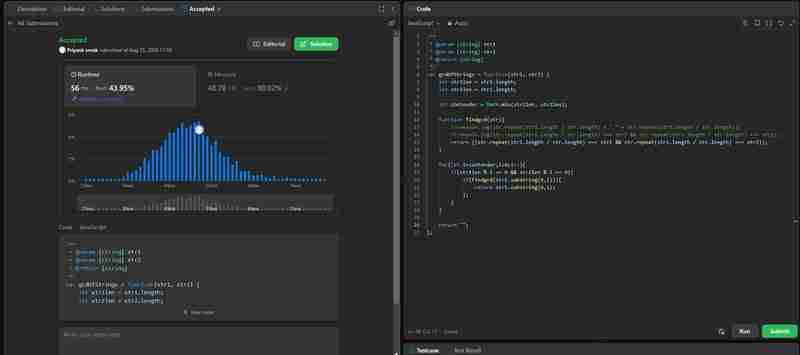
Complexité temporelle : Dans le pire des cas, nous parcourons le Min(str1,str2) et nous devons recréer str1 et str2 pour que ce soit (str1.length str2.length) donc complexité temporelle globale sera O(min(str1,str2) * (str1.length str2.length))

Complexité de l'espace : O(1) car nous n'avons pas besoin d'espace supplémentaire.