JavaScript est fréquemment ridiculisé lorsque les développeurs rencontrent pour la première fois ce résultat apparemment déroutant :

0.1   0.2 == 0.30000000000000004

Les mèmes sur la gestion des nombres par JavaScript sont très répandus, ce qui amène souvent beaucoup à croire que ce comportement est propre au langage.

Cependant, cette bizarrerie ne se limite pas à JavaScript. C'est une conséquence de la façon dont la plupart des langages de programmation gèrent l'arithmétique à virgule flottante.

Par exemple, voici des extraits de code de Java et Go qui produisent des résultats similaires :

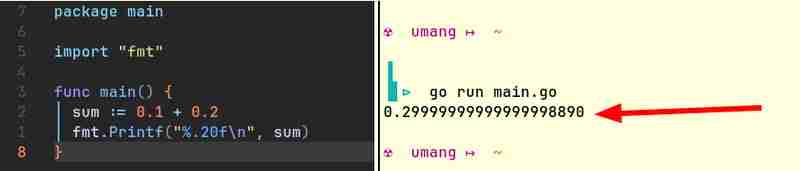
Les ordinateurs ne peuvent stocker nativement que des entiers. Ils ne comprennent pas les fractions. (Comment le feront-ils ? La seule manière pour les ordinateurs de faire du calcul est d'allumer ou d'éteindre certaines lumières. La lumière peut être allumée ou éteinte. Elle ne peut pas être « à moitié » allumée !) Ils ont besoin d'un moyen de représenter les nombres à virgule flottante. . Comme cette représentation n'est pas parfaitement précise, le plus souvent, 0,1 0,2 n'est pas égal à 0,3.

Toutes les fractions dont les dénominateurs sont constitués de facteurs premiers de la base du système numérique peuvent être exprimées proprement, tandis que toutes les autres fractions auraient des décimales répétitives. Par exemple, dans le système numérique en base 10, les fractions comme 1/2, 1/4, 1/5, 1/10 sont clairement représentées car les dénominateurs dans chaque cas sont constitués de 2 ou 5 - les facteurs premiers de 10. . Cependant, les fractions comme 1/3, 1/6, 1/7 ont toutes des décimales récurrentes.

De même, dans le système binaire, les fractions comme 1/2, 1/4, 1/8 sont exprimées proprement tandis que toutes les autres fractions ont des décimales récurrentes. Lorsque vous effectuez des opérations arithmétiques sur ces décimales récurrentes, vous vous retrouvez avec des restes qui sont conservés lorsque vous convertissez la représentation binaire des nombres de l'ordinateur en une représentation en base 10 lisible par l'homme. C'est ce qui conduit à des résultats à peu près corrects.

Maintenant que nous avons établi que ce problème n'est pas exclusif à JavaScript, explorons comment les nombres à virgule flottante sont représentés et traités sous le capot pour comprendre pourquoi ce comportement se produit.

Afin de comprendre comment les nombres à virgule flottante sont représentés et traités sous le capot, nous devons d'abord comprendre la norme à virgule flottante IEEE 754.

La norme IEEE 754 est une spécification largement utilisée pour représenter et effectuer des opérations arithmétiques sur des nombres à virgule flottante dans les systèmes informatiques. Il a été créé pour garantir la cohérence lors de l'utilisation de l'arithmétique à virgule flottante sur diverses plates-formes informatiques. La plupart des langages de programmation et des implémentations matérielles (CPU, GPU, etc.) adhèrent à cette norme.

Voici comment un nombre est indiqué au format IEEE 754 :

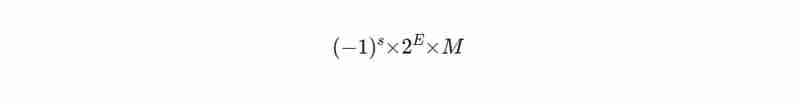
Ici s est le bit de signe (0 pour positif, 1 pour négatif), M est la mantisse (contient les chiffres du nombre) et E est l'exposant qui détermine l'échelle du nombre.

Vous ne pourrez pas trouver de valeurs entières pour M et E pouvant représenter exactement des nombres comme 0,1, 0,2 ou 0,3 dans ce format. Nous ne pouvons choisir que les valeurs pour M et E qui donnent le résultat le plus proche.

Voici un outil que vous pouvez utiliser pour déterminer les notations IEEE 754 des nombres décimaux : https://www.h-schmidt.net/FloatConverter/IEEE754.html

Notation IEEE 754 de 0,25 :

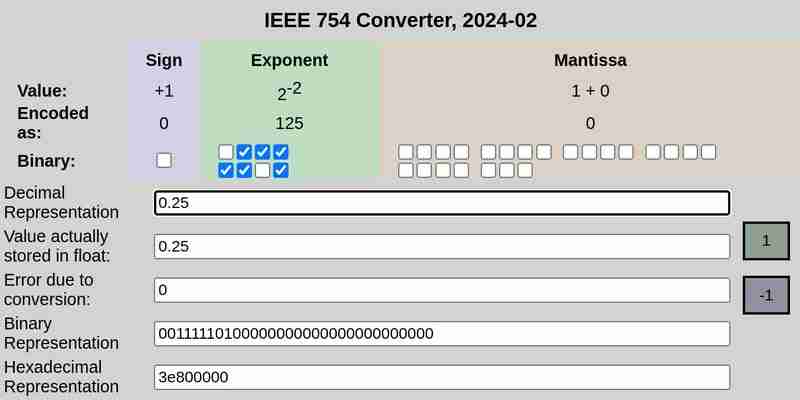
Notation IEEE 754 de 0,1 et 0,2 respectivement :

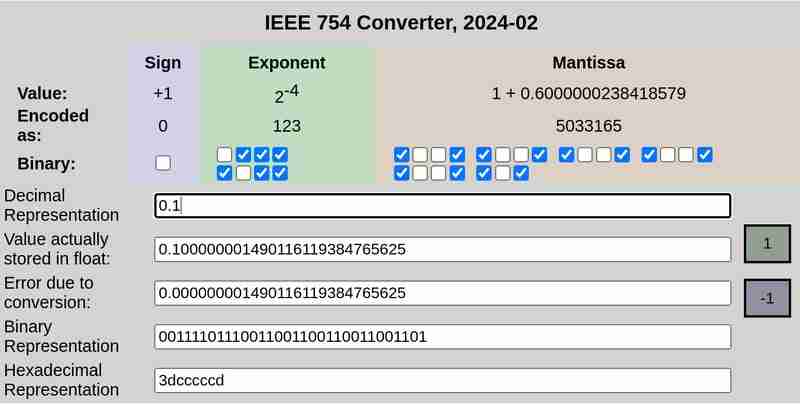
Veuillez noter que l'erreur due à la conversion dans le cas de 0,25 était de 0, tandis que 0,1 et 0,2 avaient des erreurs non nulles.

IEEE 754 définit les formats suivants pour représenter les nombres à virgule flottante :

• Simple précision (32 bits) : 1 bit pour le signe, 8 bits pour l'exposant, 23 bits pour la mantisse

• Double précision (64 bits) : 1 bit pour le signe, 11 bits pour l'exposant, 52 bits pour la mantisse

Par souci de simplicité, considérons le format simple précision qui utilise 32 bits.

La représentation 32 bits de 0,1 est :

0 01111011 10011001100110011001101

Ici, le premier bit représente le signe (0 qui signifie positif dans ce cas), les 8 bits suivants (01111011) représentent l'exposant et les 23 derniers bits (10011001100110011001101) représentent la mantisse.

Ceci n'est pas une représentation exacte. Cela représente ≈ 0,100000001490116119384765625

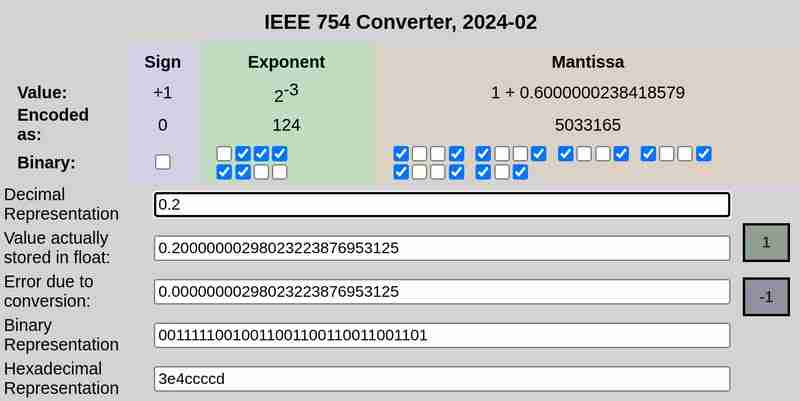
De même, la représentation 32 bits de 0,2 est :

0 01111100 10011001100110011001101

Ce n'est pas non plus une représentation exacte. Cela représente ≈ 0,20000000298023223876953125

Une fois ajouté, cela donne :

0 01111101 11001101010011001100110 

qui est ≈ 0,30000001192092896 en représentation décimale.

En conclusion, le résultat apparemment déroutant de 0,1 0,2 ne donnant pas 0,3 n'est pas une anomalie spécifique à JavaScript, mais une conséquence des limitations de l'arithmétique à virgule flottante dans les langages de programmation. Les racines de ce comportement résident dans la représentation binaire des nombres, qui conduit intrinsèquement à des erreurs de précision lors du traitement de certaines fractions.