Cette section présente des algorithmes efficaces pour trouver la paire de points la plus proche en utilisant la méthode diviser pour régner. Étant donné un ensemble de points, le problème de la paire la plus proche consiste à trouver les deux points les plus proches l’un de l’autre. Comme le montre la figure ci-dessous, une ligne est tracée pour relier les deux points les plus proches dans l'animation de la paire la plus proche.

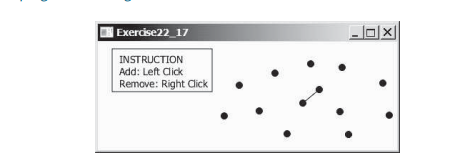
Étude de cas : Trouver la paire la plus proche, a présenté un algorithme de force brute pour trouver la paire de points la plus proche. L'algorithme calcule les distances entre toutes les paires de points et trouve celle avec la distance minimale. De toute évidence, l'algorithme prend un temps O(n^2). Pouvons-nous concevoir un algorithme plus efficace ?

Nous utiliserons une approche appelée diviser pour régner pour résoudre ce problème. L'approche divise le problème en sous-problèmes, résout les sous-problèmes, puis combine les solutions des sous-problèmes pour obtenir la solution du problème entier. Contrairement à l’approche de programmation dynamique, les sous-problèmes de l’approche diviser pour régner ne se chevauchent pas. Un sous-problème est comme le problème d'origine avec une taille plus petite, vous pouvez donc appliquer la récursivité pour résoudre le problème. En fait, toutes les solutions aux problèmes récursifs suivent l’approche diviser pour régner.

Les étapes ci-dessous décrivent comment résoudre le problème de la paire la plus proche en utilisant l'approche diviser pour régner.

• Étape 1 : Triez les points par ordre croissant de coordonnées x. Pour les points ayant les mêmes coordonnées x, triez sur les coordonnées y. Cela donne une liste triée S de points.
• Étape 2 : Divisez S en deux sous-ensembles, S1 et S2, de taille égale en utilisant le point médian de la liste triée. Soit le milieu dans S1. Trouvez récursivement la paire la plus proche dans S1 et S2. Soit d1 et d2 la distance des paires les plus proches dans les deux sous-ensembles, respectivement.
• Étape 3 : Trouvez la paire la plus proche entre un point de S1 et un point de S2 et notez leur distance par d3. La paire la plus proche est celle avec la distance min(d1, d2, d3).

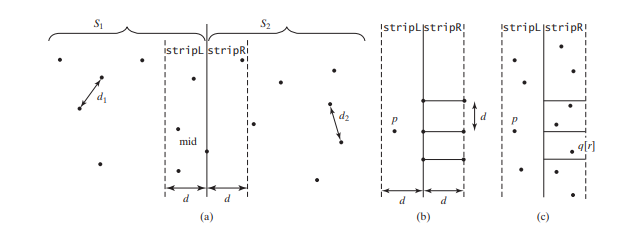
Le tri par sélection prend un temps O(n^2). L'étape 1 peut être effectuée en un temps O(n log n). L'étape 3 peut être effectuée en un temps O(n). Soit d = min(d1, d2). Nous savons déjà que la distance entre les paires les plus proches ne peut pas être supérieure à d. Pour qu'un point dans S1 et un point dans S2 forment la paire la plus proche dans S, le point gauche doit être dans stripL et le point droit dans stripR, comme illustré dans la figure ci-dessous ( un).

Pour un point p dans stripL, vous n'avez besoin de considérer qu'un point droit dans le rectangle d X 2d, comme indiqué ci-dessous (b). Tout point droit en dehors du rectangle ne peut pas former la paire la plus proche avec p. Puisque la distance entre les paires les plus proches dans S2 est supérieure ou égale à d, il peut y avoir au plus six
points dans le rectangle. Ainsi, pour chaque point de stripL, au plus six points de stripR doivent être pris en compte.

Pour chaque point p dans stripL, comment localisez-vous les points dans la zone rectangulaire d X 2d correspondante dans stripR ? Cela peut être fait efficacement si les points de stripL et stripR sont triés par ordre croissant de leurs coordonnées y. Soit pointsOrderedOnY la liste des points triés par ordre croissant de coordonnées y. pointsOrderedOnY peuvent être obtenus au préalable dans l’algorithme. stripL et stripR peuvent être obtenus à partir de pointsOrderedOnY à l'étape 3, comme indiqué dans le code ci-dessous.

pour chaque point p en pointsOrderedOnY
si (p est dans S1 et mid.x – p.x ajouter p à stripL;
sinon si (p est dans S2 et p.x - mid.x ajouter p à stripR;

Soit les points de stripL et stripR être {p0, p1, ... , pk} et {q0, q1, ... , qt}, comme indiqué dans Figure ci-dessus (c). La paire la plus proche entre un point dans stripL et un point dans stripR peut être trouvée à l'aide de l'algorithme décrit dans le code ci-dessous.

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



Les points de stripL sont considérés à partir de p0, p1, ... , pk dans cet ordre. Pour un point p dans stripL, ignorez les points dans stripR qui se trouvent en dessous de p.y – d (lignes 5 à 6). Une fois qu'un point est sauté, il ne sera plus pris en compte. La boucle while (lignes 9 à 17) vérifie si (p, q[r1]) est une paire la plus proche possible. Il existe au plus six paires q[r1], car la distance entre deux points de stripR ne peut pas être inférieure à d. Ainsi, la complexité pour trouver la paire la plus proche à l’étape 3 est O(n).

 Notez que l'étape 1 des étapes ci-dessus n'est effectuée qu'une seule fois pour pré-trier les points. Supposons que tous les points soient pré-triés. Soit T(n) la complexité temporelle de cet algorithme. Ainsi,



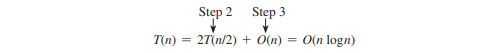
Par conséquent, la paire de points la plus proche peut être trouvée en un temps O(n log n).