Introduction

Dans cet article, nous présenterons un flux de travail complet de projet d'apprentissage automatique à l'aide de Scikit-Learn. Nous construirons un modèle pour prédire les prix des logements en Californie sur la base de diverses caractéristiques, telles que le revenu médian, l'âge de la maison et le nombre moyen de pièces. Ce projet vous guidera à travers chaque étape du processus, y compris le chargement des données, l'exploration, la formation du modèle, l'évaluation et la visualisation des résultats. Que vous soyez un débutant cherchant à comprendre les bases ou un praticien expérimenté cherchant une remise à niveau, cet article vous fournira des informations précieuses sur l'application pratique des techniques d'apprentissage automatique.

Projet de prévision des prix des logements en Californie

1. Introduction

Le marché immobilier californien est connu pour ses caractéristiques uniques et sa dynamique de prix. Dans ce projet, nous visons à développer un modèle d'apprentissage automatique pour prédire les prix de l'immobilier en fonction de diverses caractéristiques. Nous utiliserons l'ensemble de données sur le logement californien, qui comprend divers attributs tels que le revenu médian, l'âge de la maison, le nombre moyen de pièces, etc.

2. Importation de bibliothèques

Dans cette section, nous importerons les bibliothèques nécessaires à la manipulation des données, à la visualisation et à la création de notre modèle d'apprentissage automatique.

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.datasets import fetch_california_housing

3. Chargement de l'ensemble de données

Nous allons charger l'ensemble de données California Housing et créer un DataFrame pour organiser les données. La variable cible, qui est le prix de l'immobilier, sera ajoutée dans une nouvelle colonne.

# Load the California Housing dataset
california = fetch_california_housing()
df = pd.DataFrame(california.data, columns=california.feature_names)
df['PRICE'] = california.target

4. Sélection aléatoire d'échantillons

Pour que l'analyse reste gérable, nous sélectionnerons au hasard 700 échantillons de l'ensemble de données pour notre étude.

# Randomly Selecting 700 Samples
df_sample = df.sample(n=700, random_state=42)

5. Examiner nos données

Cette section fournira un aperçu de l'ensemble de données, affichant les cinq premières lignes pour comprendre les caractéristiques et la structure de nos données.

# Overview of the data
print("First five rows of the dataset:")
print(df_sample.head())

Sortir

First five rows of the dataset:
       MedInc  HouseAge  AveRooms  AveBedrms  Population  AveOccup  Latitude  \
20046  1.6812      25.0  4.192201   1.022284      1392.0  3.877437     36.06   
3024   2.5313      30.0  5.039384   1.193493      1565.0  2.679795     35.14   
15663  3.4801      52.0  3.977155   1.185877      1310.0  1.360332     37.80   
20484  5.7376      17.0  6.163636   1.020202      1705.0  3.444444     34.28   
9814   3.7250      34.0  5.492991   1.028037      1063.0  2.483645     36.62   

       Longitude    PRICE  
20046    -119.01  0.47700  
3024     -119.46  0.45800  
15663    -122.44  5.00001  
20484    -118.72  2.18600  
9814     -121.93  2.78000  

Afficher les informations du DataFrame

print(df_sample.info())

Sortir

Index: 700 entries, 20046 to 5350
Data columns (total 9 columns):
 #   Column      Non-Null Count  Dtype  
---  ------      --------------  -----  
 0   MedInc      700 non-null    float64
 1   HouseAge    700 non-null    float64
 2   AveRooms    700 non-null    float64
 3   AveBedrms   700 non-null    float64
 4   Population  700 non-null    float64
 5   AveOccup    700 non-null    float64
 6   Latitude    700 non-null    float64
 7   Longitude   700 non-null    float64
 8   PRICE       700 non-null    float64
dtypes: float64(9)
memory usage: 54.7 KB

Afficher les statistiques récapitulatives

print(df_sample.describe())

Sortir

           MedInc    HouseAge    AveRooms   AveBedrms   Population  \
count  700.000000  700.000000  700.000000  700.000000   700.000000   
mean     3.937653   28.855714    5.404192    1.079266  1387.422857   
std      2.085831   12.353313    1.848898    0.236318  1027.873659   
min      0.852700    2.000000    2.096692    0.500000     8.000000   
25%      2.576350   18.000000    4.397751    1.005934   781.000000   
50%      3.480000   30.000000    5.145295    1.047086  1159.500000   
75%      4.794625   37.000000    6.098061    1.098656  1666.500000   
max     15.000100   52.000000   36.075472    5.273585  8652.000000   

         AveOccup    Latitude   Longitude       PRICE  
count  700.000000  700.000000  700.000000  700.000000  
mean     2.939913   35.498243 -119.439729    2.082073  
std      0.745525    2.123689    1.956998    1.157855  
min      1.312994   32.590000 -124.150000    0.458000  
25%      2.457560   33.930000 -121.497500    1.218500  
50%      2.834524   34.190000 -118.420000    1.799000  
75%      3.326869   37.592500 -118.007500    2.665500  
max      7.200000   41.790000 -114.590000    5.000010  

6. Diviser l'ensemble de données en ensembles de train et de test

Nous séparerons l'ensemble de données en fonctionnalités (X) et en variable cible (y), puis le diviserons en ensembles de formation et de test pour la formation et l'évaluation du modèle.

# Splitting the dataset into Train and Test sets
X = df_sample.drop('PRICE', axis=1)  # Features
y = df_sample['PRICE']  # Target variable

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

7. Formation sur modèle

Dans cette section, nous allons créer et entraîner un modèle de régression linéaire en utilisant les données d'entraînement pour connaître la relation entre les caractéristiques et les prix de l'immobilier.

# Creating and training the Linear Regression model
lr = LinearRegression()
lr.fit(X_train, y_train)

8. Évaluation du modèle

Nous ferons des prédictions sur l'ensemble de test et calculerons l'erreur quadratique moyenne (MSE) et les valeurs R au carré pour évaluer les performances du modèle.

# Making predictions on the test set
y_pred = lr.predict(X_test)

# Calculating Mean Squared Error
mse = mean_squared_error(y_test, y_pred)
print(f"\nLinear Regression Mean Squared Error: {mse}")

Sortir

Linear Regression Mean Squared Error: 0.3699851092128846

9. Affichage des valeurs réelles et prévues

Ici, nous allons créer un DataFrame pour comparer les prix réels des logements avec les prix prévus générés par notre modèle.

# Displaying Actual vs Predicted Values
results = pd.DataFrame({'Actual Prices': y_test.values, 'Predicted Prices': y_pred})
print("\nActual vs Predicted:")
print(results)

Sortir

Actual vs Predicted:
     Actual Prices  Predicted Prices
0          0.87500          0.887202
1          1.19400          2.445412
2          5.00001          6.249122
3          2.78700          2.743305
4          1.99300          2.794774
..             ...               ...
135        1.62100          2.246041
136        3.52500          2.626354
137        1.91700          1.899090
138        2.27900          2.731436
139        1.73400          2.017134

[140 rows x

 2 columns]

10. Visualiser les résultats

Dans la dernière section, nous visualiserons la relation entre les prix réels et prévus des logements à l'aide d'un nuage de points pour évaluer visuellement les performances du modèle.

# Visualizing the Results
plt.figure(figsize=(8, 6))
plt.scatter(y_test, y_pred, color='blue')
plt.xlabel('Actual Prices')
plt.ylabel('Predicted Prices')
plt.title('Actual vs Predicted House Prices')

# Draw the ideal line
plt.plot([0, 6], [0, 6], color='red', linestyle='--')

# Set limits to minimize empty space
plt.xlim(y_test.min() - 1, y_test.max()   1)
plt.ylim(y_test.min() - 1, y_test.max()   1)

plt.grid()
plt.show()

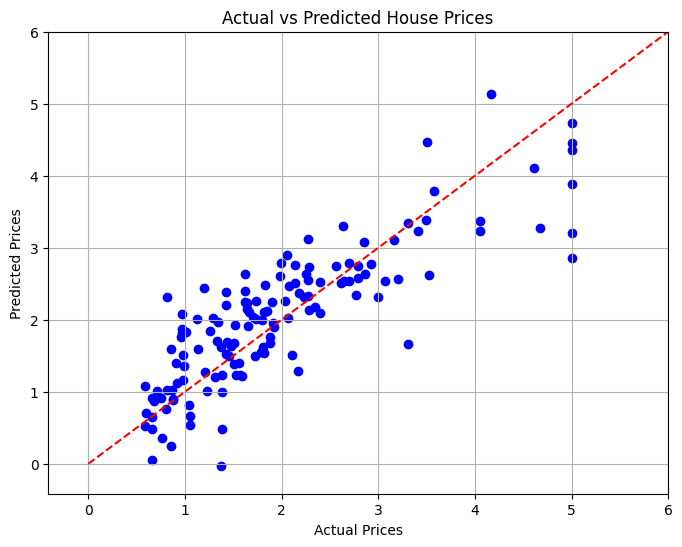
Conclusion

Dans ce projet, nous avons développé un modèle de régression linéaire pour prédire les prix des logements en Californie en fonction de diverses caractéristiques. L'erreur quadratique moyenne a été calculée pour évaluer les performances du modèle, qui a fourni une mesure quantitative de l'exactitude des prévisions. Grâce à la visualisation, nous avons pu voir les performances de notre modèle par rapport aux valeurs réelles.

Ce projet démontre la puissance de l'apprentissage automatique dans l'analyse immobilière et peut servir de base à des techniques de modélisation prédictive plus avancées.