El problema ponderado de las nueve colas se puede reducir al problema ponderado del camino más corto.
La sección presentó el problema de las nueve colas y lo resolvió utilizando el algoritmo BFS. Esta sección presenta una variación del problema y lo resuelve utilizando el algoritmo del camino más corto.

El problema de las nueve colas es encontrar el número mínimo de movimientos que lleven a que todas las monedas queden boca abajo. Cada movimiento lanza una moneda cara y sus vecinas. El problema ponderado de las nueve colas asigna el número de lanzamientos como un peso en cada movimiento. Por ejemplo, puede cambiar las monedas de la Figura siguiente a por las de la Figura siguiente b lanzando la primera moneda de la primera fila y sus dos vecinas. Por tanto, el peso de este movimiento es 3. Puedes cambiar las monedas de la Figura siguiente c a la Figura siguiente d lanzando la moneda central y sus cuatro vecinas. Entonces el peso de este movimiento es 5.

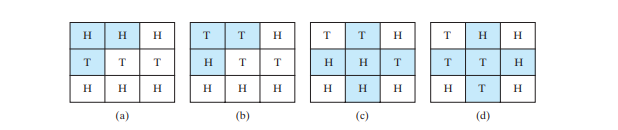
El problema de las nueve colas ponderadas se puede reducir a encontrar la ruta más corta desde un nodo inicial hasta el nodo objetivo en un gráfico ponderado por bordes. El gráfico tiene 512 nodos. Cree una arista desde el nodo v hasta u si hay un movimiento desde el nodo u hasta el nodo v. Asigna el número de giros para que sea el peso del borde.

Recuerde que en la Sección definimos una clase NineTailModel para modelar el problema de las nueve colas. Ahora definimos una nueva clase llamada WeightedNineTailModel que extiende NineTailModel, como se muestra en la siguiente figura.

La clase NineTailModel crea un Graph y obtiene un Tree con raíz en el nodo objetivo 511. WeightedNineTailModel es lo mismo que NineTailModel excepto que crea un WeightedGraph y obtiene un ShortestPathTree con raíz en el nodo de destino 511. WeightedNineTailModel extiende NineTailModel. El método getEdges() encuentra todos los bordes del gráfico. El método getNumberOfFlips(int u, int v) devuelve el número de cambios del nodo u al nodo v. El método getNumberOfFlips(int u) devuelve el número de volteos desde el nodo u al nodo objetivo.

El siguiente código implementa WeightedNineTailModel.

package demo;
import java.util.*;

public class WeightedNineTailModel extends NineTailModel {
    /** Construct a model */
    public WeightedNineTailModel() {
        // Create edges
        List edges = getEdges();

        // Create a graph
        WeightedGraph graph = new WeightedGraph(edges, NUMBER_OF_NODES);

        // Obtain a shortest path tree rooted at the target node
        tree = graph.getShortestPath(511);
    }

    /** Create all edges for the graph */
    private List getEdges() {
        // Store edges
        List edges = new ArrayList();

        for(int u = 0; u .ShortestPathTree)tree).getCost(u);
    }
}

WeightedNineTailModel extiende NineTailModel para crear un WeightedGraph para modelar el problema ponderado de nueve colas (líneas 10 a 11). Para cada nodo u, el método getEdges() encuentra un nodo volteado v y asigna el número de volteos como peso para el borde (v, u) (línea 30). El método getNumberOfFlips(int u, int v) devuelve el número de cambios del nodo u al nodo v (líneas 38–47). El número de lanzamientos es el número de celdas diferentes entre el
dos nodos (línea 44).

El WeightedNineTailModel obtiene un ShortestPathTree con raíz en el nodo de destino 511 (línea 14). Tenga en cuenta que tree es un campo de datos protegido definido en NineTailModel y ShortestPathTree es una subclase de Tree. Los métodos definidos en NineTailModel usan la propiedad tree.

El método getNumberOfFlips(int u) (líneas 49 a 52) devuelve el número de cambios desde el nodo u al nodo objetivo, que es el costo de la ruta desde el nodo u al nodo de destino. Este costo se puede obtener invocando el método getCost(u) definido en la clase ShortestPathTree (línea 51).

El siguiente código proporciona un programa que solicita al usuario que ingrese un nodo inicial y muestra el número mínimo de giros para alcanzar el nodo objetivo.

package demo;

import java.util.Scanner;

public class WeightedNineTail {

    public static void main(String[] args) {
        // Prompt the user to enter nine coins' Hs and Ts
        System.out.print("Enter the initial nine coins Hs and Ts: ");
        Scanner input = new Scanner(System.in);
        String s = input.nextLine();
        char[] initialNode = s.toCharArray();

        WeightedNineTailModel model = new WeightedNineTailModel();
        java.util.List path = model.getShortestPath(NineTailModel.getIndex(initialNode));

        System.out.println("The steps to flip the coins are ");
        for (int i = 0; i 



Ingrese nueve monedas iniciales Hs y Ts: HHHTTTHHH

Los pasos para lanzar las monedas son

HHH

TTT

HHH

HHH

THT

TTT

TTT

TTT

TTT

El número de lanzamientos es 8

El programa solicita al usuario ingresar un nodo inicial con nueve letras con una combinación de Hs y Ts como una cadena en la línea 8, obtiene una matriz de caracteres de la cadena (línea 9), crea un modelo (línea 11), obtiene la ruta más corta desde el nodo inicial al nodo de destino (líneas 12-13), muestra los nodos en la ruta (líneas 16–17) e invoca getNumberOfFlips para obtener el número de giros necesarios para alcanzar el nodo objetivo (línea 20).