Imagínese si solo pudiera usar líneas rectas, elipses y círculos, ¿no sería difícil diseñar un automóvil con líneas suaves y una apariencia compleja?

En 1962, el ingeniero francés Pierre Bézier publicó la curva de Bézier, que se utilizó inicialmente para el diseño de la carrocería principal de los automóviles.

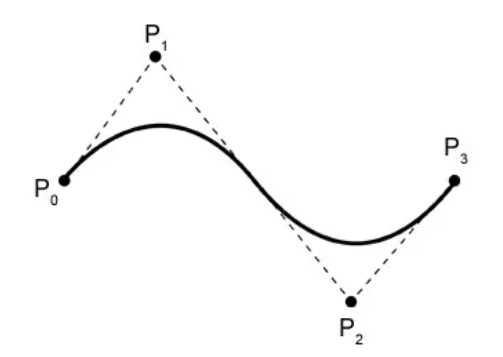
Las curvas de Bézier pueden definir una curva suave a través de una serie de puntos de control. La curva siempre pasa por el primer y último punto de control y está influenciada por la forma de los puntos de control intermedios. Además, las curvas de Bézier tienen la propiedad de tener cascos convexos.

Las curvas de Bézier se utilizan ampliamente en gráficos por computadora y modelado de imágenes, como en animación, diseño de fuentes y diseño industrial.

Fórmula

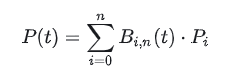
Entendamos esto.

P(t) representa un punto de la curva en t (t es una fracción, con un valor de 0 a 1). ¿Qué es un punto de la curva en t? Una descripción de curva común es: y = f(x), y por ahora, entendamos P(t) como f(x). La diferencia es que P(t) es una representación paramétrica (y el resultado del cálculo es un "vector" como [x, y]), que se explicará en detalle más adelante.

A continuación, Pi representa el i-ésimo punto de control (i comienza desde 0). Tomando la figura anterior como ejemplo, hay 4 puntos de control, que son P0, P1, P2, P3. El n en la fórmula es el último índice de los puntos de control, es decir, n = 3 (tenga en cuenta que no es el número de puntos de control, sino el recuento menos 1).

Bi,n(t) es la función de base de Bernstein, también conocida como función de base. Para cada (i, n) específico, le corresponde una función base diferente. Si lo entiende desde una perspectiva ponderada, puede considerar la función base como una función de peso, que indica la "contribución" del i-ésimo punto de control Pi a las coordenadas de la curva en la posición de t.

La fórmula de la función base es la siguiente:

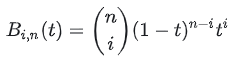
$\left(\genfrac{}{}{0px}{}{n}{i}\right)$( in​) Es el número de combinación (¿cuántas formas de elegir i entre n?). En cuanto a por qué la función base se ve así, se puede entender en relación con el algoritmo de De Casteljau (ver más adelante en el texto)

Volvamos a la fórmula P(t), ${\sum }_{i=0}^n$∑i=0n ​ es el símbolo de suma, que indica que la parte siguiente ( ${\mathrm{Papelera}}_{(t)}\cdot PiB\_\{i,n\}(t)\; \backslash cdot\; P\_i{}_{}B$i,n​(t )⋅Pi​ ) se debe sumar de i=0 a i=n. Tomando la figura anterior como ejemplo, suponiendo que queremos calcular P (0.1), ¿cómo hacerlo? Se amplía de la siguiente manera:

Sustituye t=0.1 para obtener:

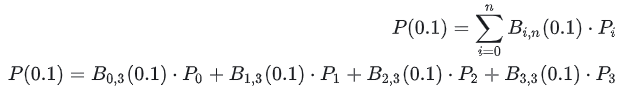
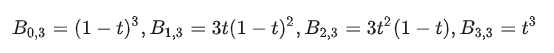Representación paramétrica de la curva.

Aquí se cita directamente un artículo de un internauta (enlace)

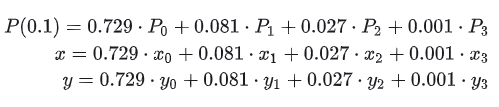
Centrémonos en la fórmula anterior.

Como se muestra en la figura anterior, la línea recta con la que estamos familiarizados se puede entender desde otra perspectiva: usando t (es decir, la longitud de |AP| desde el punto P hasta el punto conocido (x0,y0)), entonces el punto P se puede determinar mediante las funciones trigonométricas anteriores.

De manera más general, se puede escribir como: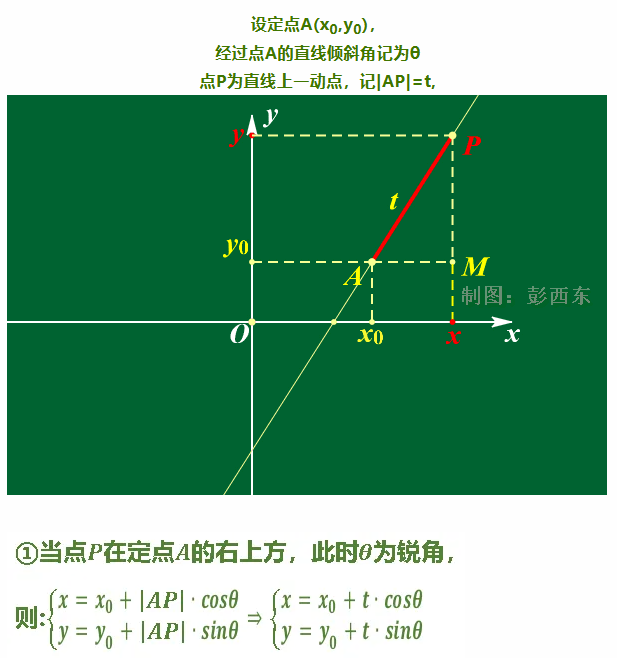

Aquí, P0 es el vector [x0,y0]y v también es un vector. Cuando se suman, P(t)es el vector [x,y].

Mirando el círculo de nuevo:

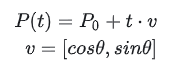
Como se muestra en el diagrama, se puede considerar que el círculo tiene un centro conocido, y cualquier punto del círculo está determinado por el ángulo de rotación y el radio. También se puede escribir como:

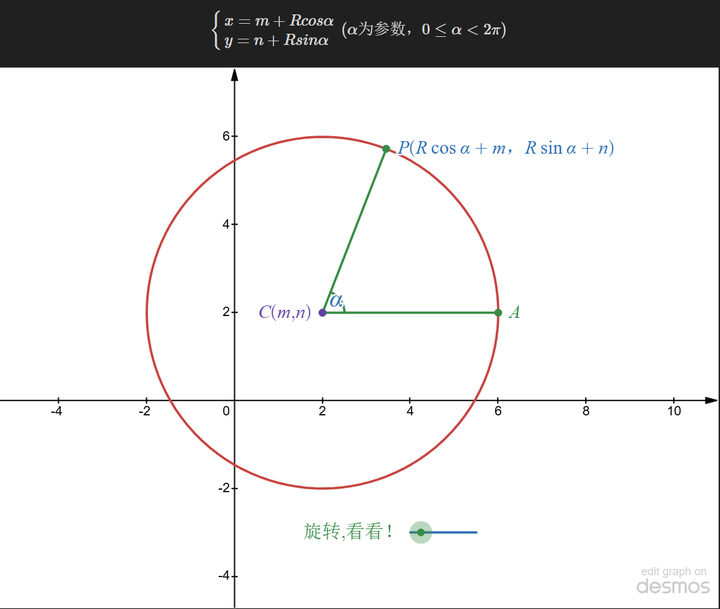Las ecuaciones paramétricas mantienen la invariancia geométrica y pueden representar formas como círculos (donde una x corresponde a múltiples valores de y).

De Casteljau

El algoritmo de De Casteljau es un método utilizado en aplicaciones prácticas para evaluar y aproximar curvas de Bézier para dibujar y otras operaciones. En comparación con el método de evaluación anterior basado en definiciones, es más rápido, más estable y más cercano a las características de las curvas de Bézier.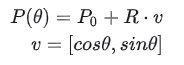

Aquí nos referimos a dos artículos: enlace1 y enlace2

Primeramente se define lo siguiente:

Mira el β anterior. Es un poco confuso con los superíndices y subíndices; puede utilizar la siguiente recursividad triangular para comprender:

Los bordes rojos del triángulo en la figura anterior son los puntos de control de los dos segmentos divididos por t0. Para comprender más vívidamente t0, P(t0) （es decir,

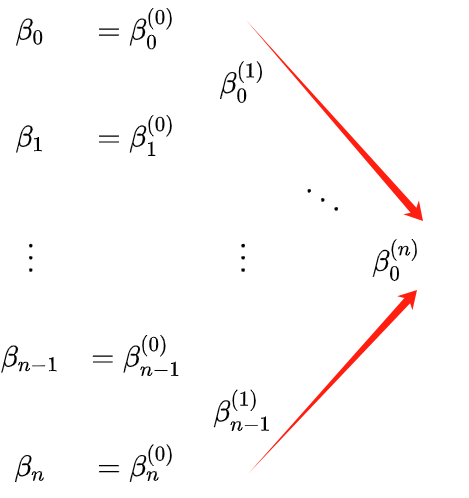
β0$(n_{\mathrm{)}}^{\backslash beta\_0^\{(n)\}}\beta$0(n)​ ）, los puntos de control de las dos curvas, puede consultar la siguiente figura: La figura anterior demuestra las relaciones entre varios puntos cuando t=0,5. Desde la perspectiva de la "interpolación", el proceso de cálculo también puede entenderse como:

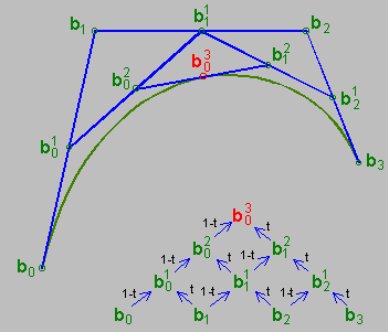Encontrar los puntos medios de cada par de puntos de control adyacentes (porque t=0.5), es decir, b01, b11, b21 (perdone mi notación; escribir en LaTeX es demasiado problemático)

Encuentre el punto medio b02 en b01-b11 y encuentre el punto medio b12 en b11-b21

Encuentra el punto medio b03 en b02−b12 ​ De hecho, la esencia del algoritmo de De Casteljau es la interpolación y la iteración.

1. Dibujo de curvas basado en De Casteljau
2. Actualmente, se observan dos métodos.
3. Un método implica atravesar t de 0 a 1 con pequeños incrementos (es decir, 0,01). Cada vez que se busca P(t), se utiliza una fórmula recursiva para determinar

β0$(n_{\mathrm{)}}^{\backslash beta\_0^\{(n)\}}\beta$0(n)​ . El otro método implica buscar P(t=0.5), y luego para las dos curvas divididas, se busca P(t=0.5) respectivamente... Esta subdivisión continúa hasta que se aproxima la curva. Implementación Siempre parece irreal simplemente mirar sin practicar.

Así que escribí mi propio código de implementación para dibujar curvas y lo organicé en un conjunto de herramientas: Compilelife's Toolkit

El código principal correspondiente está aquí