Esta sección presenta algoritmos eficientes para encontrar el par de puntos más cercano usando divide y vencerás. Dado un conjunto de puntos, el problema del par más cercano es encontrar los dos puntos más cercanos entre sí. Como se muestra en la figura siguiente, se dibuja una línea para conectar los dos puntos más cercanos en la animación del par más cercano.

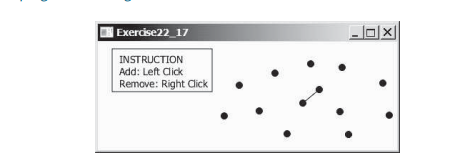
Estudio de caso: Encontrar el par más cercano, presentó un algoritmo de fuerza bruta para encontrar el par de puntos más cercano. El algoritmo calcula las distancias entre todos los pares de puntos y encuentra el que tiene la distancia mínima. Claramente, el algoritmo toma O(n^2) tiempo. ¿Podemos diseñar un algoritmo más eficiente?

Utilizaremos un enfoque llamado divide y vencerás para resolver este problema. El enfoque divide el problema en subproblemas, resuelve los subproblemas y luego combina las soluciones de los subproblemas para obtener la solución para todo el problema. A diferencia del enfoque de programación dinámica, los subproblemas del enfoque de divide y vencerás no se superponen. Un subproblema es como el problema original con un tamaño más pequeño, por lo que puedes aplicar la recursividad para resolver el problema. De hecho, todas las soluciones para problemas recursivos siguen el enfoque de divide y vencerás.

Los pasos siguientes describen cómo resolver el problema del par más cercano utilizando el enfoque de divide y vencerás.

• Paso 1: Ordena los puntos en orden creciente de coordenadas x. Para los puntos con las mismas coordenadas x, ordene según las coordenadas y. Esto da como resultado una lista ordenada S de puntos.
• Paso 2: Divida S en dos subconjuntos, S1 y S2, de igual tamaño utilizando el punto medio de la lista ordenada. Sea el punto medio en S1. Encuentre recursivamente el par más cercano en S1 y S2. Sean d1 y d2 la distancia de los pares más cercanos en los dos subconjuntos, respectivamente.
• Paso 3: Encuentra el par más cercano entre un punto en S1 y un punto en S2 y denota su distancia como d3. El par más cercano es el que tiene la distancia min(d1, d2, d3).

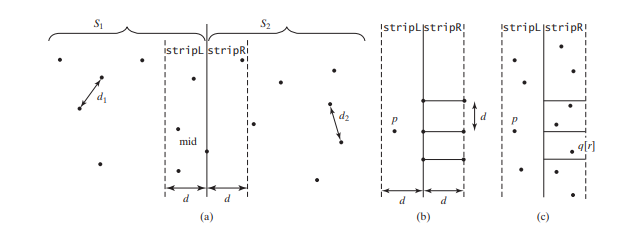
La clasificación por selección lleva O(n^2) tiempo. El paso 1 se puede realizar en tiempo O(n log n). El paso 3 se puede realizar en tiempo O(n). Sea d = mín(d1, d2). Ya sabemos que la distancia del par más cercano no puede ser mayor que d. Para que un punto en S1 y un punto en S2 formen el par más cercano en S, el punto izquierdo debe estar en stripL y el punto derecho en stripR, como se ilustra en la Figura siguiente ( a).

Para un punto p en stripL, solo necesita considerar un punto derecho dentro del rectángulo d X 2d, como se muestra a continuación (b). Cualquier punto derecho fuera del rectángulo no puede formar el par más cercano a p. Dado que la distancia del par más cercano en S2 es mayor o igual a d, puede haber como máximo seis
puntos en el rectángulo. Por lo tanto, para cada punto en stripL, se deben considerar como máximo seis puntos en stripR.

Para cada punto p en stripL, ¿cómo ubicas los puntos en el área del rectángulo d X 2d correspondiente en stripR? Esto se puede hacer de manera eficiente si los puntos en stripL y stripR se ordenan en orden creciente de sus coordenadas y. Sea pointsOrderedOnY la lista de puntos ordenados en orden creciente de coordenadas y. pointsOrderedOnY se pueden obtener de antemano en el algoritmo. stripL y stripR se pueden obtener de pointsOrderedOnY en el Paso 3 como se muestra en el código siguiente.

para cada punto p en puntosOrderedOnY
si (p está en S1 y mid.x – p.x agregar p a la tiraL;
de lo contrario si (p está en S2 y p.x - mid.x agregar p a stripR;

Sean los puntos en stripL y stripR {p0, p1, ... , pk} y {q0, q1, ... , qt}, como se muestra en Figura arriba (c). El par más cercano entre un punto en stripL y un punto en stripR se puede encontrar usando el algoritmo que se describe en el código siguiente.

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



Los puntos en stripL se consideran desde p0, p1, ..., pk en este orden. Para un punto p en stripL, omita los puntos en stripR que están debajo de p.y – d (líneas 5–6). Una vez que se omita un punto, ya no se considerará. El bucle  while (líneas 9 a 17) comprueba si (p, q[r1]) es un posible par más cercano. Hay como máximo seis pares de este tipo q[r1], porque la distancia entre dos puntos en stripR no puede ser menor que d. Entonces, la complejidad para encontrar el par más cercano en el Paso 3 es O(n).

Tenga en cuenta que el paso 1 de los pasos anteriores se realiza solo una vez para ordenar previamente los puntos. Supongamos que todos los puntos están preclasificados. Sea T(n) la complejidad temporal de este algoritmo. De este modo,



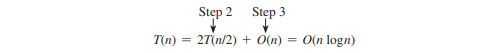
Por lo tanto, el par de puntos más cercano se puede encontrar en tiempo O(n log n).