El diseño de algoritmos consiste en desarrollar un proceso matemático para resolver un problema. El análisis de algoritmos consiste en predecir el rendimiento de un algoritmo. Los dos capítulos anteriores introdujeron estructuras de datos clásicas (listas, pilas, colas, colas de prioridad, conjuntos y mapas) y las aplicaron para resolver problemas. Este capítulo utilizará una variedad de ejemplos para presentar técnicas algorítmicas comunes (programación dinámica, divide y vencerás y retroceso) para desarrollar algoritmos eficientes.

La notación Big O obtiene una función para medir la complejidad del tiempo del algoritmo en función del tamaño de entrada. Puedes ignorar las constantes multiplicativas y los términos no dominantes en la función. Supongamos que dos algoritmos realizan la misma tarea, como la búsqueda (búsqueda lineal frente a búsqueda binaria). ¿Cuál es mejor? Para responder a esta pregunta, puede implementar estos algoritmos y ejecutar los programas para obtener el tiempo de ejecución. Pero hay dos problemas con este enfoque:

• Primero, muchas tareas se ejecutan simultáneamente en una computadora. El tiempo de ejecución de un programa en particular depende de la carga del sistema.
• En segundo lugar, el tiempo de ejecución depende de una entrada específica. Considere, por ejemplo, la búsqueda lineal y la búsqueda binaria. Si un elemento a buscar es el primero en la lista, la búsqueda lineal encontrará el elemento más rápido que la búsqueda binaria.

Es muy difícil comparar algoritmos midiendo su tiempo de ejecución. Para superar estos problemas, se desarrolló un enfoque teórico para analizar algoritmos independientes de las computadoras y de entradas específicas. Este enfoque se aproxima al efecto de un cambio en el tamaño de la entrada. De esta manera, puede ver qué tan rápido aumenta el tiempo de ejecución de un algoritmo a medida que aumenta el tamaño de entrada, por lo que puede comparar dos algoritmos examinando sus tasas de crecimiento.

Considere la búsqueda lineal. El algoritmo de búsqueda lineal compara la clave con los elementos de la matriz secuencialmente hasta que se encuentra la clave o se agota la matriz. Si la clave no está en la matriz, requiere comparaciones n para una matriz de tamaño n. Si la clave está en la matriz, requiere n/2 comparaciones en promedio. El tiempo de ejecución del algoritmo es proporcional al tamaño de la matriz. Si duplica el tamaño de la matriz, esperará que se duplique el número de comparaciones. El algoritmo crece a un ritmo lineal. La tasa de crecimiento tiene un orden de magnitud de n. Los informáticos utilizan la notación O grande para representar el "orden de magnitud". Usando esta notación, la complejidad del algoritmo de búsqueda lineal es O(n), pronunciada como "orden de n". A un algoritmo con una complejidad temporal de O(n) lo llamamos algoritmo lineal y exhibe una tasa de crecimiento lineal.

Para el mismo tamaño de entrada, el tiempo de ejecución de un algoritmo puede variar, dependiendo de la entrada. Una entrada que da como resultado el tiempo de ejecución más corto se llama la entrada del mejor de los casos, y una entrada que da como resultado el tiempo de ejecución más largo es la entrada del peor de los casos. Análisis del mejor de los casos y
El análisis del peor de los casos consiste en analizar los algoritmos para determinar su entrada en el mejor y el peor de los casos. Los análisis del mejor y del peor de los casos no son representativos, pero el análisis del peor de los casos es muy útil. Puede estar seguro de que el algoritmo nunca será más lento que en el peor de los casos.
Un análisis de caso promedio intenta determinar la cantidad de tiempo promedio entre todas las entradas posibles del mismo tamaño. El análisis de casos promedio es ideal, pero difícil de realizar, porque para muchos problemas es difícil determinar las probabilidades y distribuciones relativas de varias instancias de entrada. El análisis del peor de los casos es más fácil de realizar, por lo que generalmente se realiza para el peor de los casos.

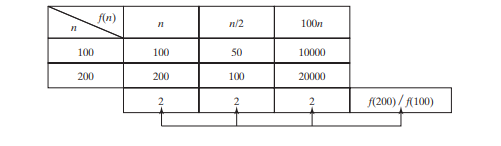
El algoritmo de búsqueda lineal requiere n comparaciones en el peor de los casos y n/2 comparaciones en el caso promedio si casi siempre busca algo que se sabe que está en la lista. Usando la notación Big O, ambos casos requieren tiempo O(n). Se puede omitir la constante multiplicativa (1/2). El análisis de algoritmos se centra en la tasa de crecimiento. Las constantes multiplicativas no tienen impacto sobre las tasas de crecimiento. La tasa de crecimiento para n/2 o 100_n_ es la misma que para n, como se ilustra en la siguiente tabla, Tasas de crecimiento. Por lo tanto, O(n) = O(n/2) = O(100n).

Considere el algoritmo para encontrar el número máximo en una matriz de n elementos. Para encontrar el número máximo si n es 2, se necesita una comparación; si n es 3, dos comparaciones. En general, se necesitan n - 1 comparaciones para encontrar el número máximo en una lista de n elementos. El análisis de algoritmos es para entradas de gran tamaño. Si el tamaño de entrada es pequeño, no hay importancia a la hora de estimar la eficiencia de un algoritmo. A medida que n crece, la parte n de la expresión n - 1 domina la complejidad. La notación O grande le permite ignorar la parte no dominante (por ejemplo, -1 en el
expresión n - 1) y resalte la parte importante (por ejemplo, n en la expresión n - 1). Por tanto, la complejidad de este algoritmo es O(n).

La notación Big O estima el tiempo de ejecución de un algoritmo en relación con el tamaño de entrada. Si el tiempo no está relacionado con el tamaño de entrada, se dice que el algoritmo toma tiempo constante con la notación O(1). Por ejemplo, un método que recupera un elemento en un índice determinado en una matriz
toma un tiempo constante, porque el tiempo no aumenta a medida que aumenta el tamaño de la matriz.

Las siguientes sumas matemáticas suelen ser útiles en el análisis de algoritmos:

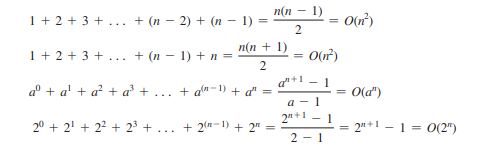
Complejidad del tiempo es una medida del tiempo de ejecución utilizando la notación Big-O. De manera similar, también puedes medir la complejidad del espacio usando la notación O grande. La complejidad del espacio mide la cantidad de espacio de memoria utilizado por un algoritmo. La complejidad espacial de la mayoría de los algoritmos presentados en el libro es O(n). es decir, exhiben una tasa de crecimiento lineal con respecto al tamaño de los insumos. Por ejemplo, la complejidad espacial para la búsqueda lineal es O(n).