La búsqueda en profundidad de un gráfico comienza desde un vértice del gráfico y visita todos los vértices del gráfico en la medida de lo posible antes de retroceder.
La búsqueda en profundidad de un gráfico es como la búsqueda en profundidad de un árbol que se analiza en Tree Traversal, Tree Traversal. En el caso de un árbol, la búsqueda comienza desde la raíz. En un gráfico, la búsqueda puede comenzar desde cualquier vértice.

Una búsqueda en profundidad de un árbol primero visita la raíz y luego visita recursivamente los subárboles de la raíz. De manera similar, la búsqueda en profundidad de un gráfico primero visita un vértice y luego visita recursivamente todos los vértices adyacentes a ese vértice. La diferencia es que el gráfico puede contener ciclos, lo que podría conducir a una recursión infinita. Para evitar este problema, debe realizar un seguimiento de los vértices que ya han sido visitados.

La búsqueda se llama primero en profundidad porque busca “más profundamente” en el gráfico tanto como sea posible. La búsqueda comienza desde algún vértice v. Después de visitar v, visita un vecino no visitado de v. Si v no tiene un vecino no visitado, la búsqueda retrocede hasta el vértice desde el cual llegó a v. Suponemos que el gráfico está conectado y la búsqueda comienza desde cualquier vértice se puede llegar a todos los vértices.

Algoritmo de búsqueda en profundidad

El algoritmo para la búsqueda en profundidad se describe en el siguiente código.

Entrada: G = (V, E) y un vértice inicial v
Salida: un árbol DFS con raíz en v
1 árbol dfs (vértice v) {
2 visita v;
3 por cada vecino w de v
4 si (w no ha sido visitado) {
5 establezca v como padre de w en el árbol;
6 dfs(w);
7 }
8 }

Puede utilizar una matriz denominada isVisited para indicar si se ha visitado un vértice. Inicialmente, isVisited[i] es falso para cada vértice i. Una vez que se visita un vértice, digamos v, isVisited[v] se establece en true.

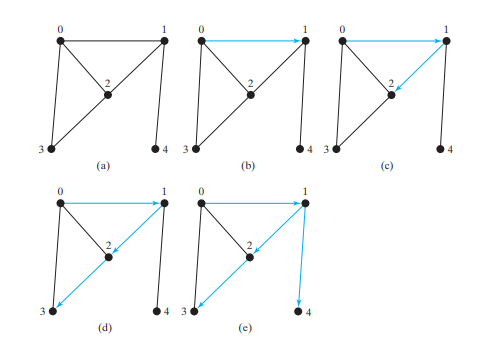
Considere el gráfico de la figura siguiente (a). Supongamos que comenzamos la búsqueda en profundidad desde el vértice 0. Primero visitamos 0, luego cualquiera de sus vecinos, digamos 1. Ahora se visita 1, como se muestra en la Figura siguiente (b). El vértice 1 tiene tres vecinos: 0, 2 y 4. Como ya se visitó 0, visitará 2 o 4. Elijamos 2. Ahora se visita 2, como se muestra en la Figura siguiente (c). El vértice 2 tiene tres vecinos: 0, 1 y 3. Dado que 0 y 1 ya han sido visitados, seleccione 3. Ahora se visita 3, como se muestra en la Figura siguiente (d). Hasta este punto, los vértices han sido visitados en este orden:

0, 1, 2, 3

Como se han visitado todos los vecinos de 3, retroceda hasta 2. Como se han visitado todos los vértices de 2, retroceda hasta 1. 4 es adyacente a 1, pero 4 no ha sido visitado. Por lo tanto, visite 4, como se muestra en la Figura siguiente (e). Como todos los vecinos de 4 han sido visitados, retroceda a 1.
Como se han visitado todos los vecinos de 1, retroceda a 0. Como se han visitado todos los vecinos de 0, la búsqueda finaliza.

Dado que cada borde y cada vértice se visita solo una vez, la complejidad temporal del método dfs es O(|E| |V|), donde |E | denota el número de aristas y |V| el número de vértices.

Implementación de la búsqueda en profundidad

El algoritmo para DFS en el código anterior utiliza recursividad. Es natural utilizar la recursividad para implementarlo. Alternativamente, puedes usar una pila.

El método dfs(int v) se implementa en las líneas 164–193 en AbstractGraph.java. Devuelve una instancia de la clase Tree con el vértice v como raíz. El método almacena los vértices buscados en la lista searchOrder (línea 165), el padre de cada vértice en la matriz parent (línea 166), y utiliza el método isVisited matriz para indicar si se ha visitado un vértice (línea 171). Invoca el método auxiliar dfs(v, parent, searchOrder, isVisited) para realizar una búsqueda en profundidad (línea 174).

En el método auxiliar recursivo, la búsqueda comienza desde el vértice u. u se agrega a searchOrder en la línea 184 y se marca como visitado (línea 185). Para cada vecino no visitado de u, el método se invoca de forma recursiva para realizar una búsqueda en profundidad. Cuando se visita un vértice e.v, el padre de e.v se almacena en parent[e.v] (línea 189). El método regresa cuando se visitan todos los vértices de un gráfico conectado o de un componente conectado.

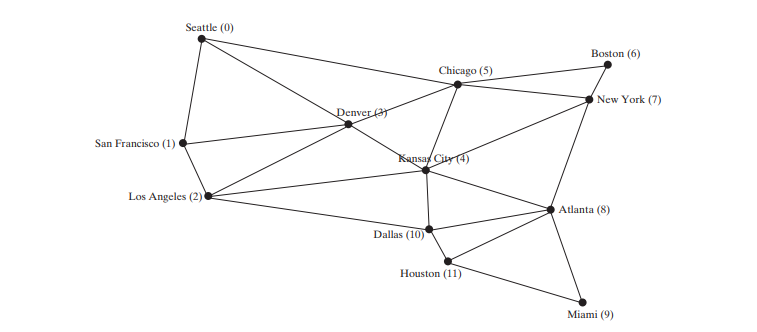
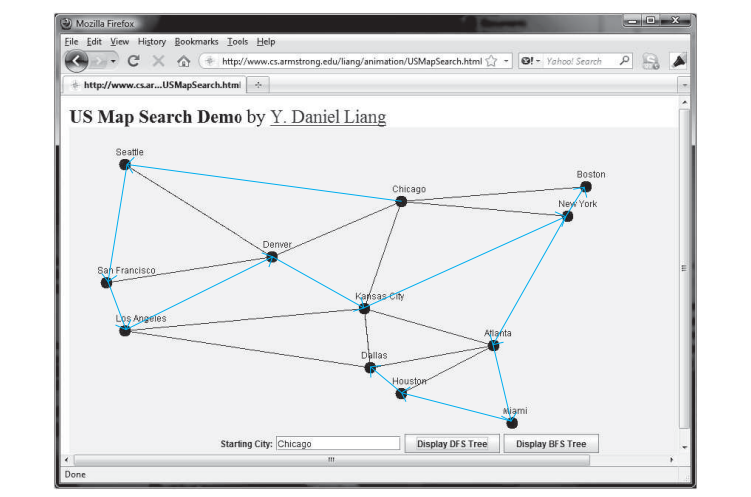
El siguiente código proporciona un programa de prueba que muestra un DFS para el gráfico de la figura anterior comenzando desde Chicago. La ilustración gráfica del DFS comenzando desde Chicago se muestra en la siguiente figura.

public class TestDFS {

    public static void main(String[] args) {
        String[] vertices = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York", "Atlanta", "Miami", "Dallas", "Houston"};

        int[][] edges = {
                {0, 1}, {0, 3}, {0, 5},
                {1, 0}, {1, 2}, {1, 3},
                {2, 1}, {2, 3}, {2, 4}, {2, 10},
                {3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
                {4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
                {5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
                {6, 5}, {6, 7},
                {7, 4}, {7, 5}, {7, 6}, {7, 8},
                {8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
                {9, 8}, {9, 11},
                {10, 2}, {10, 4}, {10, 8}, {10, 11},
                {11, 8}, {11, 9}, {11, 10}
        };

        Graph graph = new UnweightedGraph(vertices, edges);
        AbstractGraph.Tree dfs = graph.dfs(graph.getIndex("Chicago"));

        java.util.List searchOrders = dfs.getSearchOrder();
        System.out.println(dfs.getNumberOfVerticesFound()   " vertices are searched in this DFS order:");
        for(int i = 0; i 



Se buscan 12 vértices en este orden DFS:

 Chicago Seattle San Francisco Los Ángeles Denver

 Kansas City Nueva York Boston Atlanta Miami Houston Dallas

La matriz de Seattle es Chicago

El padre de San Francisco es Seattle

La matriz de Los Ángeles es San Francisco

El padre de Denver es Los Ángeles

La matriz de Kansas City es Denver

La matriz de Boston es Nueva York

La matriz de Nueva York es Kansas City

La matriz de Atlanta es Nueva York

El padre de Miami es Atlanta

El padre de Dallas es Houston

El padre de Houston es Miami




  
  
  Aplicaciones del DFS


La búsqueda en profundidad se puede utilizar para resolver muchos problemas, como los siguientes:

Detectando si un gráfico está conectado. Busca el gráfico a partir de cualquier vértice. Si el número de vértices buscados es el mismo que el número de vértices del gráfico, el gráfico está conectado. De lo contrario, el gráfico no está conectado.
Detectando si existe un camino entre dos vértices.
Encontrar un camino entre dos vértices.
Encontrar todos los componentes conectados. Un componente conectado es un subgrafo conectado máximo en el que cada par de vértices está conectado por una ruta.
Detectando si hay un ciclo en el gráfico.
Encontrar un ciclo en el gráfico.
Encontrar una ruta/ciclo hamiltoniano. Una ruta hamiltoniana en un gráfico es una ruta que visita cada vértice del gráfico exactamente una vez. Un ciclo hamiltoniano visita cada vértice del gráfico exactamente una vez y regresa al vértice inicial.
Los primeros seis problemas se pueden resolver fácilmente utilizando el método dfs en AbstractGraph.java. Para encontrar un camino/ciclo hamiltoniano, hay que explorar todos los DFS posibles para encontrar el que conduzca al camino más largo. El camino/ciclo hamiltoniano tiene muchas aplicaciones, incluso para resolver el conocido problema del Knight's Tour.