¿Alguna vez te has preguntado por qué los casinos siempre parecen ganar? En “Superando las probabilidades: Las matemáticas detrás de las ganancias de los casinos”, exploraremos las matemáticas simples y las estrategias inteligentes que garantizan que los casinos ganen dinero a largo plazo. A través de ejemplos fáciles de entender y simulaciones de Monte Carlo, revelaremos los secretos detrás de la fachada de la casa. ¡Prepárate para descubrir cómo los casinos inclinan las probabilidades a su favor!

Comprender la ventaja de la casa

La ventaja de la casa es un concepto fundamental en el mundo de los casinos. Representa el beneficio medio que el casino espera obtener de cada apuesta realizada por los jugadores. Básicamente, es el porcentaje de cada apuesta que el casino retendrá a largo plazo.

La ventaja de la casa existe porque los casinos no pagan las apuestas ganadoras de acuerdo con las “probabilidades reales” del juego. Las probabilidades verdaderas representan la probabilidad real de que ocurra un evento. Al pagar con probabilidades ligeramente más bajas, los casinos se aseguran de obtener ganancias con el tiempo.

La ventaja de la casa (HE) se define como la ganancia del casino expresada como porcentaje de la apuesta original del jugador.

** Ruleta Europea** tiene solo un cero verde, lo que le da 37 números en total. Si un jugador apuesta 1 dólar al rojo, tiene una probabilidad de 18/37 de ganar 1 dólar y una probabilidad de 19/37 de perder 1 dólar. El valor esperado es:

Valor esperado=( 1 × 18/37 ​) ( −1 × 19/37 ​)= 18/37​ − 19/37​ = −1/37 ​≈ −2.7%

Por lo tanto, en la ruleta europea la ventaja de la casa (HE) es de alrededor del 2,7%.

Hagamos nuestro propio juego para entenderlo mejor, un juego de tirada de dados simple.

import random

def roll_dice():
    roll = random.randint(1, 100)

    if roll == 100:
        print(roll, 'You rolled a 100 and lost. Better luck next time!')
        return False
    elif roll 

En este juego:

• El jugador tiene una probabilidad de 1/100 de perder si la tirada es 100.

• El jugador tiene una probabilidad de 50/100 de perder si la tirada está entre 1 y 50.

• El jugador tiene una probabilidad de 49/100 de ganar si la tirada está entre 51 y 99.

Valor esperado =(1× 49/100​) ( −1× 51/100​) = 49/100​ − 51/100 ​= −2/100 ​ ≈ −2%

Por lo tanto, la ventaja de la casa es el 2%.

Comprender la simulación de Montecarlo

Las simulaciones de Monte Carlo son una poderosa herramienta que se utiliza para comprender y predecir sistemas complejos mediante la ejecución de numerosas simulaciones de un proceso y la observación de los resultados. En el contexto de los casinos, las simulaciones de Monte Carlo pueden modelar varios escenarios de apuestas para mostrar cómo la ventaja de la casa garantiza la rentabilidad a largo plazo. Exploremos cómo funcionan las simulaciones de Monte Carlo y cómo se pueden aplicar a un juego de casino simple.

¿Qué es una simulación de Montecarlo?

Una simulación Monte Carlo implica generar variables aleatorias para simular un proceso varias veces y analizar los resultados. Al realizar miles o incluso millones de iteraciones, podemos obtener una distribución de posibles resultados y obtener información sobre la probabilidad de diferentes eventos.

Aplicación de la simulación Monte Carlo al juego de tirada de dados

Usaremos una simulación de Monte Carlo para modelar el juego de tirada de dados que analizamos anteriormente. Esto nos ayudará a comprender cómo la ventaja de la casa afecta la rentabilidad del juego a lo largo del tiempo.

`def monte_carlo_simulation(trials):
    wins = 0
    losses = 0

    for _ in range(trials):
        if roll_dice():
            wins  = 1
        else:
            losses  = 1

    win_percentage = (wins / trials) * 100
    loss_percentage = (losses / trials) * 100
    houseEdge= loss_percentage-win_percentage
    print(f"After {trials} trials:")
    print(f"Win percentage: {win_percentage:.2f}%")
    print(f"Loss percentage: {loss_percentage:.2f}%")
    print(f"House Edge: {houseEdge:.2f}%")

# Run the simulation with 10,000,000 trials
monte_carlo_simulation(10000000)`

Interpretación de los resultados

En esta simulación, ejecutamos el juego de tirada de dados 10.000.000 de veces para observar los porcentajes de ganancias y pérdidas. Dada la ventaja de la casa calculada anteriormente (2%), esperamos que el porcentaje de pérdidas sea ligeramente mayor que el porcentaje de ganancias.

Después de ejecutar la simulación, es posible que veas resultados como:

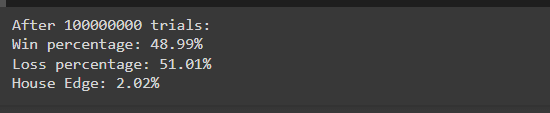
Estos resultados se alinean estrechamente con las probabilidades teóricas (49% de victoria, 51% de pérdida), lo que demuestra cómo la ventaja de la casa se manifiesta en una gran cantidad de pruebas. El ligero desequilibrio asegura la rentabilidad del casino a largo plazo.

Visualización de ganancias a corto plazo y pérdidas a largo plazo

Las simulaciones de Monte Carlo son poderosas para modelar y predecir resultados mediante muestreo aleatorio repetido. En el contexto de los juegos de azar, podemos utilizar simulaciones de Monte Carlo para comprender los resultados potenciales de diferentes estrategias de apuestas.

Simularemos a un único apostador que realiza la misma apuesta inicial en cada ronda y observaremos cómo evoluciona el valor de su cuenta a lo largo de un número específico de apuestas.

Así es como podemos simular y visualizar el proceso de apuestas usando Matplotlib:

def bettor_simulation(funds, initial_wager, wager_count):
    value = funds
    wager = initial_wager

    # Lists to store wager count and account value
    wX = []
    vY = []

    current_wager = 1

    while current_wager 



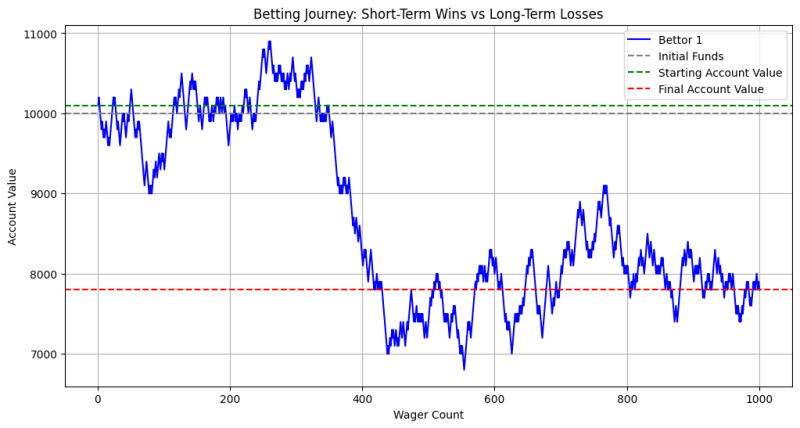
Este gráfico ilustra cómo el valor de la cuenta de un apostador puede fluctuar con el tiempo debido a ganancias y pérdidas. Inicialmente, puede haber períodos de ganancia (línea verde sobre el valor inicial), pero a medida que aumenta el número de apuestas, el efecto acumulativo de la ventaja de la casa se vuelve evidente. Con el tiempo, el valor de la cuenta del apostante tiende a disminuir hacia o por debajo de los fondos iniciales (línea gris), lo que indica pérdidas a largo plazo.


  
  
  Conclusión


Comprender las matemáticas detrás de las ganancias de los casinos revela una clara ventaja para la casa en cada juego a través del concepto de ventaja de la casa. A pesar de las ganancias ocasionales, la probabilidad incorporada en los juegos de casino garantiza que la mayoría de los jugadores perderán dinero con el tiempo. Las simulaciones de Monte Carlo ilustran vívidamente esta dinámica, mostrando cómo incluso las ganancias a corto plazo pueden enmascarar pérdidas a largo plazo debido a la ventaja estadística del casino. Esta comprensión de la certeza matemática de la rentabilidad de los casinos subraya la importancia de una toma de decisiones informada y prácticas de juego responsables.

A continuación, podríamos explorar visualizaciones o variaciones adicionales, como comparar diferentes estrategias de apuestas o analizar el impacto de diferentes apuestas iniciales en los resultados del apostador.

Mantente conectado:

• GitHub: ezhillragesh

• Twitter: ezhillragesh

• Sitio web: ragesh.me

No dudes en compartir tus pensamientos, hacer preguntas y contribuir al debate.

¡Feliz codificación!