Rekursion ist eine Technik, die zu eleganten Lösungen für Probleme führt, die mit einfachen Schleifen schwer zu programmieren sind. Angenommen, Sie möchten alle Dateien in einem Verzeichnis finden, die ein bestimmtes Wort enthalten. Wie lösen Sie dieses Problem? Dafür gibt es mehrere Möglichkeiten. Eine intuitive und effektive Lösung ist die Verwendung der Rekursion durch rekursives Durchsuchen der Dateien in den Unterverzeichnissen.

H-Bäume, dargestellt in der Abbildung unten, werden in einem VLSI-Design (Very Large Scale Integration) als Taktverteilungsnetzwerk verwendet, um Zeitsignale mit gleichen Ausbreitungsverzögerungen an alle Teile eines Chips weiterzuleiten. Wie schreibt man ein Programm zur Anzeige von H-Bäumen? Ein guter Ansatz ist die Verwendung von Rekursion.

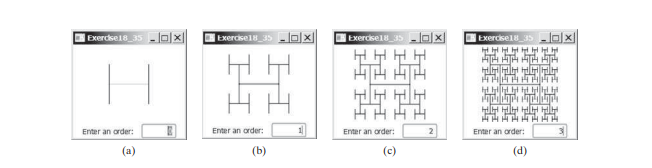
Rekursion zu verwenden bedeutet, mit rekursiven Methoden zu programmieren – das heißt, Methoden zu verwenden, die sich selbst aufrufen. Rekursion ist eine nützliche Programmiertechnik. In manchen Fällen ermöglicht es Ihnen, eine natürliche, unkomplizierte und einfache Lösung für ein ansonsten schwieriges Problem zu entwickeln.