Wie weit können Sie ein Programm zur Berechnung der Fibonacci-Folge optimieren?

Einführung

Als ich Python lernte, gab uns unser Lehrer eine Hausaufgabe: Berechnen Sie die N-te Zahl der Fibonacci-Folge.

Ich denke, es ist sehr einfach, also schreibe ich diesen Code:

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n - 1)   fib(n - 2)

Später weiß ich, dass diese Art von Lösung zu viel Zeit kostet.

Optimieren Sie ein Programm

Ich ändere die Lösung in Iteration.

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1] ls[i-2])

    return ls[n-1]

Ich verwende Matplotlib, um die Zeit zu zeichnen, die es kostet:

import time
import matplotlib.pyplot as plt


def bench_mark(func, *args):
    # calculate the time
    start = time.perf_counter()
    result = func(*args)
    end = time.perf_counter()

    return end - start, result  # return the time and the result

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1] ls[i-2])

    return ls[n-1]

mark_list = []

for i in range(1,10000):
    mark = bench_mark(fib,i)
    mark_list.append(mark[0])
    print(f"size : {i} , time : {mark[0]}")

plt.plot(range(1, 10000), mark_list)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (seconds)')
plt.title('Test fot fibonacci')
plt.grid(True)
plt.show()

Ergebnis hier:

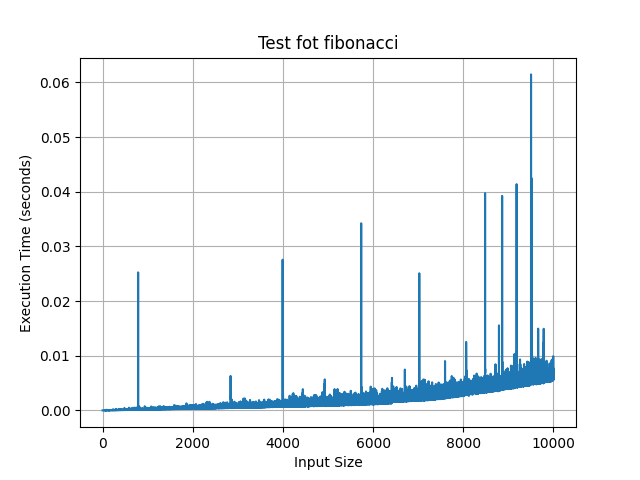
Die Zeit, die es kostet, ist sehr kurz.

Aber ich schreibe fib(300000), kostet 5,719049899998936 Sekunden. Es ist zu lang.

Wenn ich groß bin, lerne ich CACHE, also ändere ich die Lösung, um dict zum Speichern des Ergebnisses zu verwenden.

from functools import lru_cache
@lru_cache(maxsize=None)
def fib(n):
    if n 



Oder wir können den CACHE selbst schreiben.


def fib(n, cache={}):
    if n in cache:
        return cache[n]
    elif n