JavaScript wird häufig lächerlich gemacht, wenn Entwickler zum ersten Mal auf dieses scheinbar verwirrende Ergebnis stoßen:

0.1   0.2 == 0.30000000000000004

Memes über den Umgang von JavaScript mit Zahlen sind weit verbreitet, was viele oft zu der Annahme verleitet, dass dieses Verhalten nur in der Sprache vorkommt.

Diese Eigenart ist jedoch nicht nur auf JavaScript beschränkt. Dies ist eine Folge davon, wie die meisten Programmiersprachen mit Gleitkomma-Arithmetik umgehen.

Hier sind zum Beispiel Codeausschnitte aus Java und Go, die ähnliche Ergebnisse liefern:

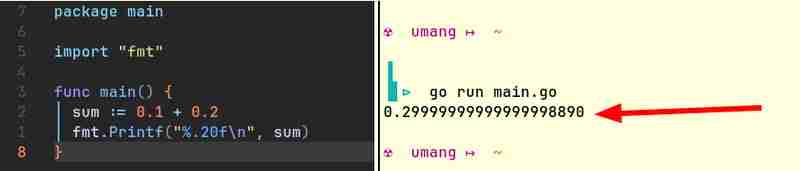
Computer können nativ nur Ganzzahlen speichern. Sie verstehen keine Brüche. (Wie wollen sie? Computer können nur rechnen, indem sie einige Lichter ein- oder ausschalten. Das Licht kann entweder an oder aus sein. Es kann nicht „halb“ an sein!) Sie brauchen eine Möglichkeit, Gleitkommazahlen darzustellen . Da diese Darstellung nicht ganz genau ist, ist 0,1 0,2 in den meisten Fällen nicht gleich 0,3.

Alle Brüche, deren Nenner aus Primfaktoren der Basis des Zahlensystems bestehen, können sauber ausgedrückt werden, während alle anderen Brüche sich wiederholende Dezimalstellen hätten. Beispielsweise werden im Zahlensystem mit der Basis 10 Brüche wie 1/2, 1/4, 1/5, 1/10 sauber dargestellt, da die Nenner jeweils aus 2 oder 5 – den Primfaktoren von 10 – bestehen . Brüche wie 1/3, 1/6, 1/7 haben jedoch alle wiederkehrende Dezimalstellen.

Ähnlich werden im Binärsystem Brüche wie 1/2, 1/4, 1/8 sauber ausgedrückt, während alle anderen Brüche wiederkehrende Dezimalstellen haben. Wenn Sie mit diesen wiederkehrenden Dezimalzahlen rechnen, bleiben am Ende Reste übrig, die übertragen werden, wenn Sie die binäre Zahlendarstellung des Computers in eine für Menschen lesbare Basis-10-Darstellung umwandeln. Dies führt zu annähernd korrekten Ergebnissen.

Da wir nun festgestellt haben, dass dieses Problem nicht nur bei JavaScript auftritt, wollen wir untersuchen, wie Gleitkommazahlen unter der Haube dargestellt und verarbeitet werden, um zu verstehen, warum dieses Verhalten auftritt.

Um zu verstehen, wie Gleitkommazahlen unter der Haube dargestellt und verarbeitet werden, müssen wir zunächst den Gleitkommastandard IEEE 754 verstehen.

Der IEEE 754-Standard ist eine weit verbreitete Spezifikation zur Darstellung und Durchführung von Arithmetik auf Gleitkommazahlen in Computersystemen. Es wurde entwickelt, um die Konsistenz bei der Verwendung der Gleitkomma-Arithmetik auf verschiedenen Computerplattformen zu gewährleisten. Die meisten Programmiersprachen und Hardwareimplementierungen (CPUs, GPUs usw.) halten sich an diesen Standard.

So wird eine Zahl im IEEE 754-Format bezeichnet:

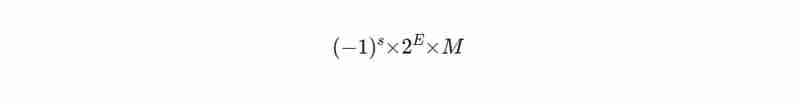
Hier ist s das Vorzeichenbit (0 für positiv, 1 für negativ), M ist die Mantisse (enthält die Ziffern der Zahl) und E ist der Exponent, der die Skalierung der Zahl bestimmt.

Sie könnten keine ganzzahligen Werte für M und E finden, die Zahlen wie 0,1, 0,2 oder 0,3 in diesem Format genau darstellen können. Wir können nur Werte für M und E auswählen, die das nächstgelegene Ergebnis liefern.

Hier ist ein Tool, mit dem Sie die IEEE 754-Notationen von Dezimalzahlen bestimmen können: https://www.h-schmidt.net/FloatConverter/IEEE754.html

IEEE 754 Notation von 0,25:

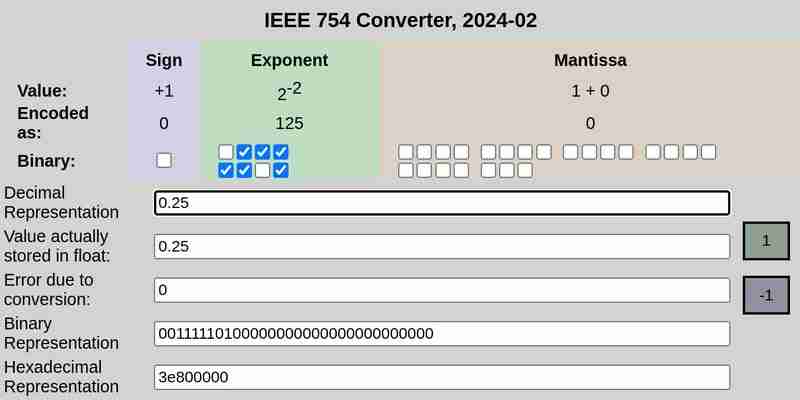
IEEE 754 Notation von 0,1 bzw. 0,2:

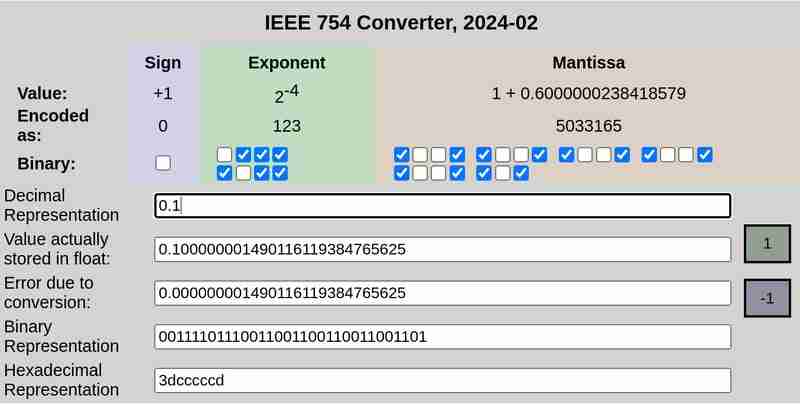
Bitte beachten Sie, dass der Fehler aufgrund der Konvertierung im Fall von 0,25 0 war, während 0,1 und 0,2 Fehler ungleich Null aufwiesen.

IEEE 754 definiert die folgenden Formate für die Darstellung von Gleitkommazahlen:

• Einfache Genauigkeit (32 Bit): 1 Bit für Vorzeichen, 8 Bit für Exponent, 23 Bit für Mantisse

• Doppelte Genauigkeit (64-Bit): 1 Bit für Vorzeichen, 11 Bit für Exponent, 52 Bit für Mantisse

Der Einfachheit halber betrachten wir das Format mit einfacher Genauigkeit, das 32 Bit verwendet.

Die 32-Bit-Darstellung von 0,1 ist:

0 01111011 10011001100110011001101

Hier stellt das erste Bit das Vorzeichen dar (0, was in diesem Fall positiv bedeutet), die nächsten 8 Bits (01111011) stellen den Exponenten dar und die letzten 23 Bits (10011001100110011001101) stellen die Mantisse dar.

Dies ist keine exakte Darstellung. Es repräsentiert ≈ 0,100000001490116119384765625

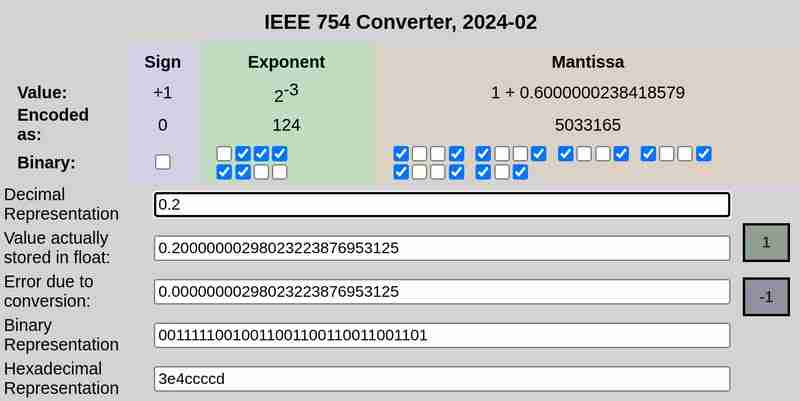
In ähnlicher Weise lautet die 32-Bit-Darstellung von 0,2:

0 01111100 10011001100110011001101

Dies ist auch keine exakte Darstellung. Es repräsentiert ≈ 0,20000000298023223876953125

Beim Hinzufügen ergibt sich Folgendes:

0 01111101 11001101010011001100110 

was ≈ 0,30000001192092896 in Dezimaldarstellung ist.

Zusammenfassend lässt sich sagen, dass das scheinbar verwirrende Ergebnis, dass 0,1 0,2 nicht 0,3 ergibt, keine für JavaScript spezifische Anomalie ist, sondern eine Folge der Einschränkungen der Gleitkomma-Arithmetik in allen Programmiersprachen. Die Wurzeln dieses Verhaltens liegen in der binären Darstellung von Zahlen, die zwangsläufig zu Präzisionsfehlern bei der Verarbeitung bestimmter Brüche führt.