Viele reale Probleme können mithilfe von Graphalgorithmen gelöst werden. Diagramme sind nützlich bei der Modellierung und Lösung realer Probleme. Das Problem, die geringste Anzahl von Flügen zwischen zwei Städten zu ermitteln, kann beispielsweise mithilfe eines Diagramms modelliert werden, bei dem die Eckpunkte Städte und die Kanten die Flüge zwischen zwei benachbarten Städten darstellen, wie in der folgenden Abbildung dargestellt. Das Problem, die minimale Anzahl von Anschlussflügen zu finden
zwischen zwei Städten reduziert sich auf die Suche nach dem kürzesten Weg zwischen zwei Eckpunkten in einem Diagramm.

Das Studium von Graphenproblemen ist als Graphentheorie bekannt. Die Graphentheorie wurde 1736 von Leonhard Euler begründet, als er die Graphenterminologie einführte, um das berühmte Problem der Sieben Brücken von Königsberg zu lösen. Die Stadt Königsberg in Preußen (heute Kaliningrad, Russland) wurde durch den Fluss Pregel geteilt. Es gab zwei Inseln am Fluss. Die Stadt und die Inseln waren durch sieben Brücken verbunden, wie in Abbildung unten (a) dargestellt. Die Frage ist: Kann man einen Spaziergang machen, jede Brücke genau einmal überqueren und zum Ausgangspunkt zurückkehren? Euler hat bewiesen, dass dies nicht möglich ist.

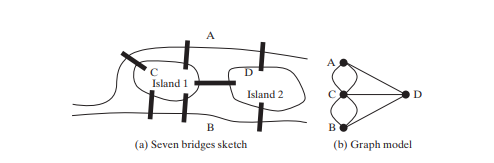
Um einen Beweis zu erbringen, abstrahierte Euler zunächst den Stadtplan von Königsberg, indem er alle Straßen eliminierte und so die in Abbildung oben (a) gezeigte Skizze erstellte. Als nächstes ersetzte er jede Landmasse durch einen Punkt, der als Scheitelpunkt oder Knoten bezeichnet wird, und jede Brücke durch eine Linie, die als Kante bezeichnet wird, wie in gezeigt Abbildung oben (b). Diese Struktur mit Eckpunkten und Kanten wird als Graph bezeichnet.

Wenn wir uns das Diagramm ansehen, fragen wir, ob es einen Pfad gibt, der an einem beliebigen Scheitelpunkt beginnt, alle Kanten genau einmal durchquert und zum Startscheitelpunkt zurückkehrt. Euler hat bewiesen, dass jeder Scheitelpunkt eine gerade Anzahl von Kanten haben muss, damit ein solcher Pfad existiert. Daher gibt es für das Problem der Sieben Brücken von Königsberg keine Lösung.

Grafikprobleme werden häufig mithilfe von Algorithmen gelöst. Graphalgorithmen haben viele Anwendungen in verschiedenen Bereichen, beispielsweise in der Informatik, Mathematik, Biologie, Ingenieurwesen, Wirtschaft, Genetik und Sozialwissenschaften.

Grundlegende Graphterminologien

Ein Graph besteht aus Scheitelpunkten und Kanten, die die Scheitelpunkte verbinden. In diesem Kapitel wird nicht davon ausgegangen, dass Sie über Vorkenntnisse in Graphentheorie oder diskreter Mathematik verfügen. Wir verwenden einfache Begriffe, um Diagramme zu definieren.

Was ist ein Diagramm? Ein Graph ist eine mathematische Struktur, die Beziehungen zwischen Entitäten in der realen Welt darstellt. Die Grafik in Abbildung oben stellt beispielsweise die Flüge zwischen Städten dar, und die Grafik in Abbildung unten (b) stellt die Brücken zwischen Landmassen dar.

Ein Graph besteht aus einer nicht leeren Menge von Scheitelpunkten (auch als Knoten oder Punkte bezeichnet) und einer Menge von Kanten, die die Scheitelpunkte verbinden. Der Einfachheit halber definieren wir einen Graphen als G = (V, E), wobei V eine Menge von Eckpunkten und E eine Menge von Kanten darstellt. Beispielsweise lauten V und E für das Diagramm in der Abbildung unten wie folgt:

V = {"Seattle", "San Francisco", "Los Angeles",
„Denver“, „Kansas City“, „Chicago“, „Boston“, „New York“,
„Atlanta“, „Miami“, „Dallas“, „Houston“};

E = {{"Seattle", "San Francisco"},{"Seattle", "Chicago"},
{"Seattle", "Denver"}, {"San Francisco", "Denver"},
...
};

Ein Graph kann gerichtet oder ungerichtet sein. In einem gerichteten Diagramm hat jede Kante eine Richtung, die angibt, dass Sie sich durch die Kante von einem Scheitelpunkt zum anderen bewegen können. Sie können Eltern-Kind-Beziehungen mithilfe eines gerichteten Diagramms modellieren, wobei eine Kante vom Scheitelpunkt A nach B angibt, dass A ein übergeordnetes Element von B ist. Die folgende Abbildung (a) zeigt einen gerichteten Graphen.

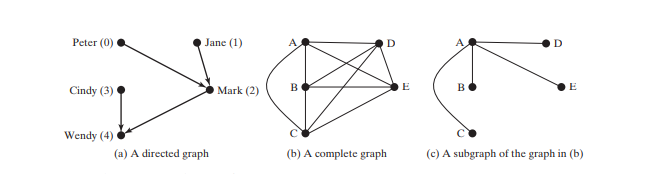
In einem ungerichteten Diagramm können Sie sich in beide Richtungen zwischen den Eckpunkten bewegen. Der Graph in der Abbildung unten ist ungerichtet.

Kanten können gewichtet oder ungewichtet sein. Sie können beispielsweise jeder Kante im Diagramm in der Abbildung oben eine Gewichtung zuweisen, um die Flugzeit zwischen den beiden Städten anzugeben.

Zwei Scheitelpunkte in einem Diagramm werden als benachbart bezeichnet, wenn sie durch dieselbe Kante verbunden sind. Ebenso werden zwei Kanten als benachbart bezeichnet, wenn sie mit demselben Scheitelpunkt verbunden sind. Eine Kante in einem Diagramm, die zwei Eckpunkte verbindet, wird als Inzident mit beiden Eckpunkten bezeichnet. Der Grad eines Scheitelpunkts ist die Anzahl der zu ihm inzidenten Kanten.

Zwei Scheitelpunkte werden Nachbarn genannt, wenn sie benachbart sind. Ebenso werden zwei Kanten als Nachbarn bezeichnet, wenn sie benachbart sind.

Eine Schleife ist eine Kante, die einen Scheitelpunkt mit sich selbst verbindet. Wenn zwei Eckpunkte durch zwei oder mehr Kanten verbunden sind, werden diese Kanten als parallele Kanten bezeichnet. Ein einfacher Graph ist ein Graph, der keine Schleifen oder parallelen Kanten hat. In einem vollständigen Diagramm sind alle zwei Scheitelpunktpaare verbunden, wie in Abbildung unten (b) dargestellt.

Ein Diagramm ist verbunden, wenn zwischen zwei beliebigen Eckpunkten im Diagramm ein Pfad vorhanden ist. Ein Untergraph eines Graphen G ist ein Graph, dessen Scheitelpunktmenge eine Teilmenge der von G ist und dessen Kantenmenge eine Teilmenge der von G ist. Beispielsweise ist der Graph in Abbildung oben (c) a Untergraph des Diagramms in Abbildung oben (b).

Angenommen, der Graph ist zusammenhängend und ungerichtet. Ein Zyklus ist ein geschlossener Pfad, der an einem Scheitelpunkt beginnt und am selben Scheitelpunkt endet. Ein verbundener Graph ist ein Baum, wenn er keine Zyklen hat. Ein spannender Baum eines Graphen G ist ein verbundener Untergraph von G und der Untergraph ist ein Baum, der alle Eckpunkte in G enthält.