In diesem Abschnitt werden effiziente Algorithmen zum Finden des nächstgelegenen Punktpaars mithilfe der Divide-and-Conquer-Methode vorgestellt. Bei einer gegebenen Menge von Punkten besteht das Problem des engsten Paares darin, die beiden Punkte zu finden, die einander am nächsten liegen. Wie in der Abbildung unten gezeigt, wird eine Linie gezeichnet, um die beiden nächstgelegenen Punkte in der Animation des nächsten Paares zu verbinden.

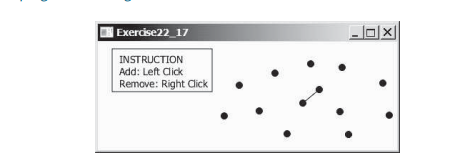
Fallstudie: Das nächstliegende Paar finden, stellte einen Brute-Force-Algorithmus zum Finden des nächstliegenden Punktepaars vor. Der Algorithmus berechnet die Abstände zwischen allen Punktpaaren und findet dasjenige mit dem minimalen Abstand. Offensichtlich benötigt der Algorithmus O(n^2) Zeit. Können wir einen effizienteren Algorithmus entwerfen?

Wir werden einen Ansatz namens Teile und herrsche verwenden, um dieses Problem zu lösen. Der Ansatz unterteilt das Problem in Teilprobleme, löst die Teilprobleme und kombiniert dann die Lösungen der Teilprobleme, um die Lösung für das gesamte Problem zu erhalten. Im Gegensatz zum dynamischen Programmieransatz überschneiden sich die Teilprobleme beim Divide-and-Conquer-Ansatz nicht. Ein Teilproblem ähnelt dem ursprünglichen Problem, hat jedoch eine kleinere Größe, sodass Sie zur Lösung des Problems eine Rekursion anwenden können. Tatsächlich folgen alle Lösungen für rekursive Probleme dem Divide-and-Conquer-Ansatz.

Die folgenden Schritte beschreiben, wie Sie das Problem des nächsten Paares mithilfe des Divide-and-Conquer-Ansatzes lösen.

• Schritt 1: Sortieren Sie die Punkte in aufsteigender Reihenfolge der x-Koordinaten. Sortieren Sie die Punkte mit denselben X-Koordinaten nach Y-Koordinaten. Dies führt zu einer sortierten Liste S von Punkten.
• Schritt 2: Teilen Sie S in zwei Teilmengen, S1 und S2, gleicher Größe auf, indem Sie den Mittelpunkt in der sortierten Liste verwenden. Der Mittelpunkt sei in S1. Finden Sie rekursiv das nächste Paar in S1 und S2. d1 und d2 bezeichnen jeweils den Abstand der nächsten Paare in den beiden Teilmengen.
• Schritt 3: Finden Sie das nächstgelegene Paar zwischen einem Punkt in S1 und einem Punkt in S2 und bezeichnen Sie deren Abstand als d3. Das nächste Paar ist das mit dem Abstand min(d1, d2, d3).

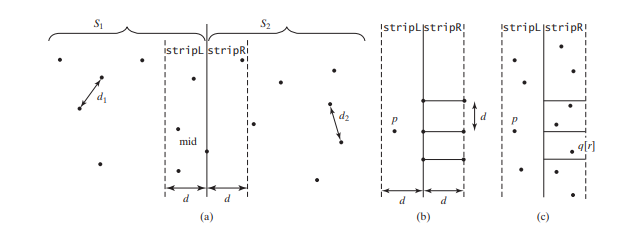
Die Auswahlsortierung benötigt O(n^2) Zeit. Schritt 1 kann in O(n log n) Zeit durchgeführt werden. Schritt 3 kann in O(n)-Zeit durchgeführt werden. Sei d = min(d1, d2). Wir wissen bereits, dass der Abstand des nächsten Paars nicht größer als d sein kann. Damit ein Punkt in S1 und ein Punkt in S2 das nächste Paar in S bilden, muss der linke Punkt in stripL und der rechte Punkt in stripR liegen, wie in der Abbildung unten dargestellt ( A).

Für einen Punkt p in stripL müssen Sie nur einen rechten Punkt innerhalb des d X 2d-Rechtecks ​​berücksichtigen, wie unten (b) gezeigt. Jeder rechte Punkt außerhalb des Rechtecks ​​kann nicht das nächstliegende Paar mit p bilden. Da der Abstand des nächsten Paares in S2 größer oder gleich d ist, kann es höchstens sechs geben
Punkte im Rechteck. Somit müssen für jeden Punkt in stripL höchstens sechs Punkte in stripR berücksichtigt werden.

Wie lokalisieren Sie für jeden Punkt p in stripL die Punkte im entsprechenden d X 2d-Rechteckbereich in stripR? Dies kann effizient durchgeführt werden, wenn die Punkte in stripL und stripR in aufsteigender Reihenfolge ihrer y-Koordinaten sortiert werden. Sei pointsOrderedOnY die Liste der Punkte, sortiert in aufsteigender Reihenfolge der y-Koordinaten. pointsOrderedOnY kann vorher im Algorithmus abgerufen werden. stripL und stripR können von pointsOrderedOnY in Schritt 3 abgerufen werden, wie im folgenden Code gezeigt.

für jeden Punkt p in pointsOrderedOnY
if (p ist in S1 und mid.x – p.x p an StripL anhängen;
sonst wenn (p ist in S2 und p.x - mid.x p an StripR anhängen;

Die Punkte in stripL und stripR seien {p0, p1, ... , pk} und {q0, q1, ... , qt}, wie in gezeigt Abbildung oben (c). Das nächstgelegene Paar zwischen einem Punkt in stripL und einem Punkt in stripR kann mithilfe des im folgenden Code beschriebenen Algorithmus gefunden werden.

d = min(d1, d2);
 r = 0; // r is the index of a point in stripR
 for (each point p in stripL) {
 // Skip the points in stripR below p.y - d
  while (r 



Die Punkte in stripL werden ab p0, p1, ..., pk in dieser Reihenfolge berücksichtigt. Überspringen Sie für einen Punkt p in stripL die Punkte in stripR, die unter p.y – d liegen (Zeilen 5–6). Sobald ein Punkt übersprungen wird, wird er nicht mehr berücksichtigt. Die while-Schleife (Zeilen 9–17) prüft, ob (p, q[r1]) ein mögliches nächstliegendes Paar ist. Es gibt höchstens sechs solcher q[r1]-Paare, da der Abstand zwischen zwei Punkten in stripR nicht kleiner als d sein kann. Die Komplexität zum Finden des nächsten Paares in Schritt 3 beträgt also O(n).

Beachten Sie, dass Schritt 1 in den obigen Schritten nur einmal ausgeführt wird, um die Punkte vorzusortieren. Gehen Sie davon aus, dass alle Punkte vorsortiert sind. T(n) bezeichne die Zeitkomplexität für diesen Algorithmus. Daher,



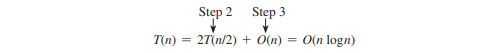
Daher kann das nächstgelegene Punktpaar in O(n log n) Zeit gefunden werden.