Algorithmusdesign ist die Entwicklung eines mathematischen Prozesses zur Lösung eines Problems. Bei der Algorithmusanalyse geht es darum, die Leistung eines Algorithmus vorherzusagen. In den beiden vorangegangenen Kapiteln wurden klassische Datenstrukturen (Listen, Stapel, Warteschlangen, Prioritätswarteschlangen, Mengen und Karten) vorgestellt und zur Lösung von Problemen angewendet. In diesem Kapitel werden anhand verschiedener Beispiele gängige algorithmische Techniken (dynamische Programmierung, Divide-and-Conquer und Backtracking) zur Entwicklung effizienter Algorithmen vorgestellt.

Die Big-O-Notation erhält eine Funktion zum Messen der Zeitkomplexität des Algorithmus basierend auf der Eingabegröße. Sie können multiplikative Konstanten und nicht dominierende Terme in der Funktion ignorieren. Angenommen, zwei Algorithmen führen dieselbe Aufgabe aus, beispielsweise eine Suche (lineare Suche vs. binäre Suche). Welches ist besser? Um diese Frage zu beantworten, könnten Sie diese Algorithmen implementieren und die Programme ausführen, um Ausführungszeit zu erhalten. Bei diesem Ansatz gibt es jedoch zwei Probleme:

• Erstens werden viele Aufgaben gleichzeitig auf einem Computer ausgeführt. Die Ausführungszeit eines bestimmten Programms hängt von der Systemlast ab.
• Zweitens hängt die Ausführungszeit von der spezifischen Eingabe ab. Betrachten Sie beispielsweise die lineare Suche und die binäre Suche. Wenn ein zu durchsuchendes Element zufällig das erste in der Liste ist, findet die lineare Suche das Element schneller als die binäre Suche.

Es ist sehr schwierig, Algorithmen durch Messung ihrer Ausführungszeit zu vergleichen. Um diese Probleme zu überwinden, wurde ein theoretischer Ansatz entwickelt, um Algorithmen unabhängig von Computern und spezifischen Eingaben zu analysieren. Dieser Ansatz nähert sich der Auswirkung einer Änderung auf die Größe der Eingabe an. Auf diese Weise können Sie sehen, wie schnell die Ausführungszeit eines Algorithmus mit zunehmender Eingabegröße zunimmt, sodass Sie zwei Algorithmen vergleichen können, indem Sie ihre Wachstumsraten untersuchen.

Erwägen Sie die lineare Suche. Der lineare Suchalgorithmus vergleicht den Schlüssel nacheinander mit den Elementen im Array, bis der Schlüssel gefunden wird oder das Array erschöpft ist. Wenn sich der Schlüssel nicht im Array befindet, sind n Vergleiche für ein Array der Größe n erforderlich. Wenn sich der Schlüssel im Array befindet, sind im Durchschnitt n/2 Vergleiche erforderlich. Die Ausführungszeit des Algorithmus ist proportional zur Größe des Arrays. Wenn Sie die Größe des Arrays verdoppeln, können Sie damit rechnen, dass sich die Anzahl der Vergleiche verdoppelt. Der Algorithmus wächst linear. Die Wachstumsrate liegt in der Größenordnung von n. Informatiker verwenden die Big-O-Notation, um die „Größenordnung“ darzustellen. Unter Verwendung dieser Notation beträgt die Komplexität des linearen Suchalgorithmus O(n), ausgesprochen als „Ordnung von n.“ Wir nennen einen Algorithmus mit einer Zeitkomplexität von O(n) einen linearen Algorithmus und er weist eine lineare Wachstumsrate auf.

Bei gleicher Eingabegröße kann die Ausführungszeit eines Algorithmus je nach Eingabe variieren. Eine Eingabe, die zur kürzesten Ausführungszeit führt, wird als Best-Case-Eingabe bezeichnet, und eine Eingabe, die zur längsten Ausführungszeit führt, ist die Worst-Case-Eingabe. Best-Case-Analyse und
Bei der Worst-Case-Analyse werden die Algorithmen hinsichtlich ihrer Best-Case-Eingabe und Worst-Case-Eingabe analysiert. Best-Case- und Worst-Case-Analysen sind nicht repräsentativ, die Worst-Case-Analyse ist jedoch sehr nützlich. Sie können sicher sein, dass der Algorithmus niemals langsamer sein wird als im schlimmsten Fall.
Eine Durchschnittsfallanalyse versucht, die durchschnittliche Zeitdauer aller möglichen Eingaben derselben Größe zu bestimmen. Eine Durchschnittsfallanalyse ist ideal, aber schwierig durchzuführen, da es bei vielen Problemen schwierig ist, die relativen Wahrscheinlichkeiten und Verteilungen verschiedener Eingabeinstanzen zu bestimmen. Die Worst-Case-Analyse ist einfacher durchzuführen, daher wird die Analyse im Allgemeinen für den Worst-Case durchgeführt.

Der lineare Suchalgorithmus erfordert im schlimmsten Fall n Vergleiche und im durchschnittlichen Fall n/2 Vergleiche, wenn Sie fast immer nach etwas suchen, von dem bekannt ist, dass es in der Liste enthalten ist. Bei Verwendung der Big-O-Notation benötigen beide Fälle O(n)-Zeit. Die multiplikative Konstante (1/2) kann weggelassen werden. Die Algorithmusanalyse konzentriert sich auf die Wachstumsrate. Die multiplikativen Konstanten haben keinen Einfluss auf die Wachstumsraten. Die Wachstumsrate für n/2 oder 100_n_ ist dieselbe wie für n, wie in der folgenden Tabelle dargestellt: Wachstumsraten. Daher ist O(n) = O(n/2) = O(100n).

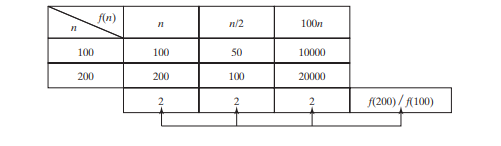
Betrachten Sie den Algorithmus zum Ermitteln der maximalen Anzahl in einem Array mit n Elementen. Um die maximale Anzahl zu ermitteln, wenn n 2 ist, ist ein Vergleich erforderlich. wenn n 3 ist, zwei Vergleiche. Im Allgemeinen sind n–1 Vergleiche erforderlich, um die maximale Anzahl in einer Liste mit n Elementen zu ermitteln. Die Algorithmusanalyse ist für große Eingabegrößen vorgesehen. Wenn die Eingabegröße klein ist, hat die Schätzung der Effizienz eines Algorithmus keine Bedeutung. Wenn n größer wird, dominiert der n-Teil im Ausdruck n - 1 die Komplexität. Mit der Big-O-Notation können Sie den nicht dominierenden Teil ignorieren (z. B. -1 im
Ausdruck n - 1) und markieren Sie den wichtigen Teil (z. B. n im Ausdruck n - 1). Daher beträgt die Komplexität dieses Algorithmus O(n).

Die Big-O-Notation schätzt die Ausführungszeit eines Algorithmus im Verhältnis zur Eingabegröße. Wenn die Zeit nicht mit der Eingabegröße zusammenhängt, sagt man, dass der Algorithmus konstante Zeit mit der Notation O(1) annimmt. Beispielsweise eine Methode, die ein Element an einem bestimmten Index in einem Array abruft
benötigt eine konstante Zeit, da die Zeit nicht mit zunehmender Größe des Arrays wächst.

Die folgenden mathematischen Summierungen sind bei der Algorithmusanalyse oft nützlich:

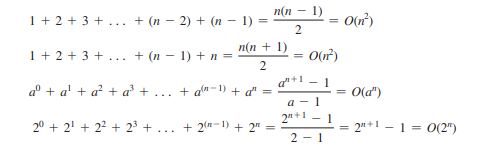
Zeitkomplexität ist ein Maß für die Ausführungszeit unter Verwendung der Big-O-Notation. In ähnlicher Weise können Sie auch die Raumkomplexität mithilfe der Big-O-Notation messen. Speicherplatzkomplexität misst die Menge an Speicherplatz, die von einem Algorithmus verwendet wird. Die Raumkomplexität für die meisten im Buch vorgestellten Algorithmen beträgt O(n). Das heißt, sie weisen eine lineare Wachstumsrate zur Eingabegröße auf. Beispielsweise beträgt die Raumkomplexität für die lineare Suche O(n).